What Does Gravity Have to Do with K-2 Math? (why above/below is easier to learn than left/right)

“A little to the left . . . no, the left . . . not your left, my left!” Even adults get into this confusing situation at times, so imagine how tricky relative positions are for children! While above/below and in front of/behind come fairly easily, left/right relationships are much more challenging.
Have you ever wondered why? In this post, we’ll explain this fun math quirk.
In kindergarten, students learn about the relative position of objects in accordance with Standard K.G.A.1:
Describe objects in the environment using names of shapes, and describe the relative positions of these objects using terms such as above, below, beside, in front of, behind, and next to.
The position of any object can only be described in relation to other objects – it’s impossible to describe the position of a single isolated object (at least in kindergarten terms). Therefore, we use the three basic planes of three-dimensional space on which objects can be related. The relative position in each plane can be described with three conceptual pairs:
1. Above – Below
2. In front of – Behind
3. Left – Right
2. In front of – Behind
3. Left – Right
Each of these pairs implies a specific perspective. For example, the red ball is situated in front of the blue ball from the point of view of the dog; but from the point of view of the cat, the red ball is located behind the blue one.

The reason above/below and in front/behind are easier for children to learn than left/right is because this implied perspective is much clearer.
Above/below is the simplest of these relative position pairs because there’s really no choice — it comes down to gravity. As astronauts experience firsthand in space, аbove/bеlow loses its meaning. But while our class is here on Earth, we assume the perspective of аbove/bеlow in response to gravity.
Students first learn to identify a position on this plane:
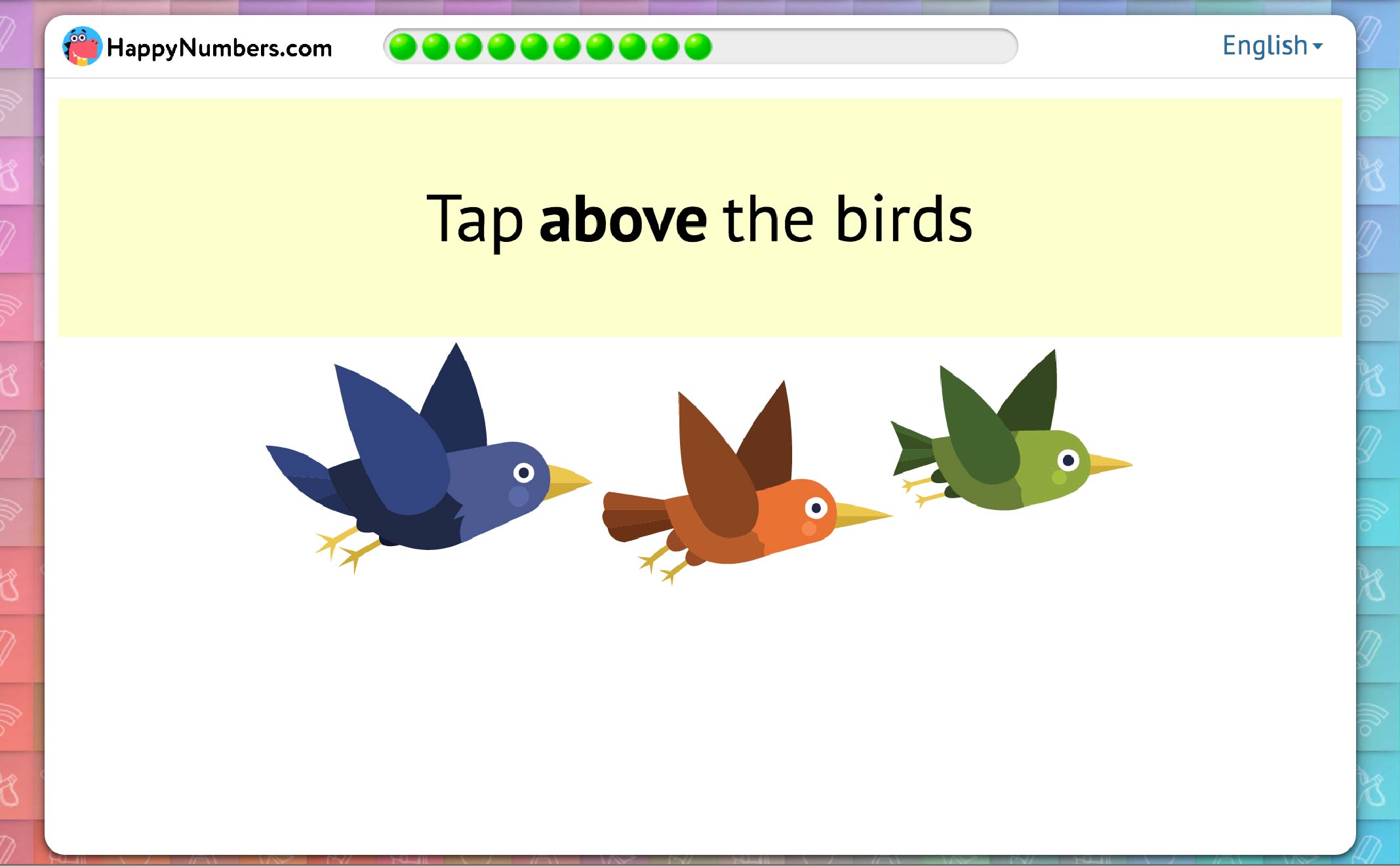
Then they can describe the position of one object relative to another:
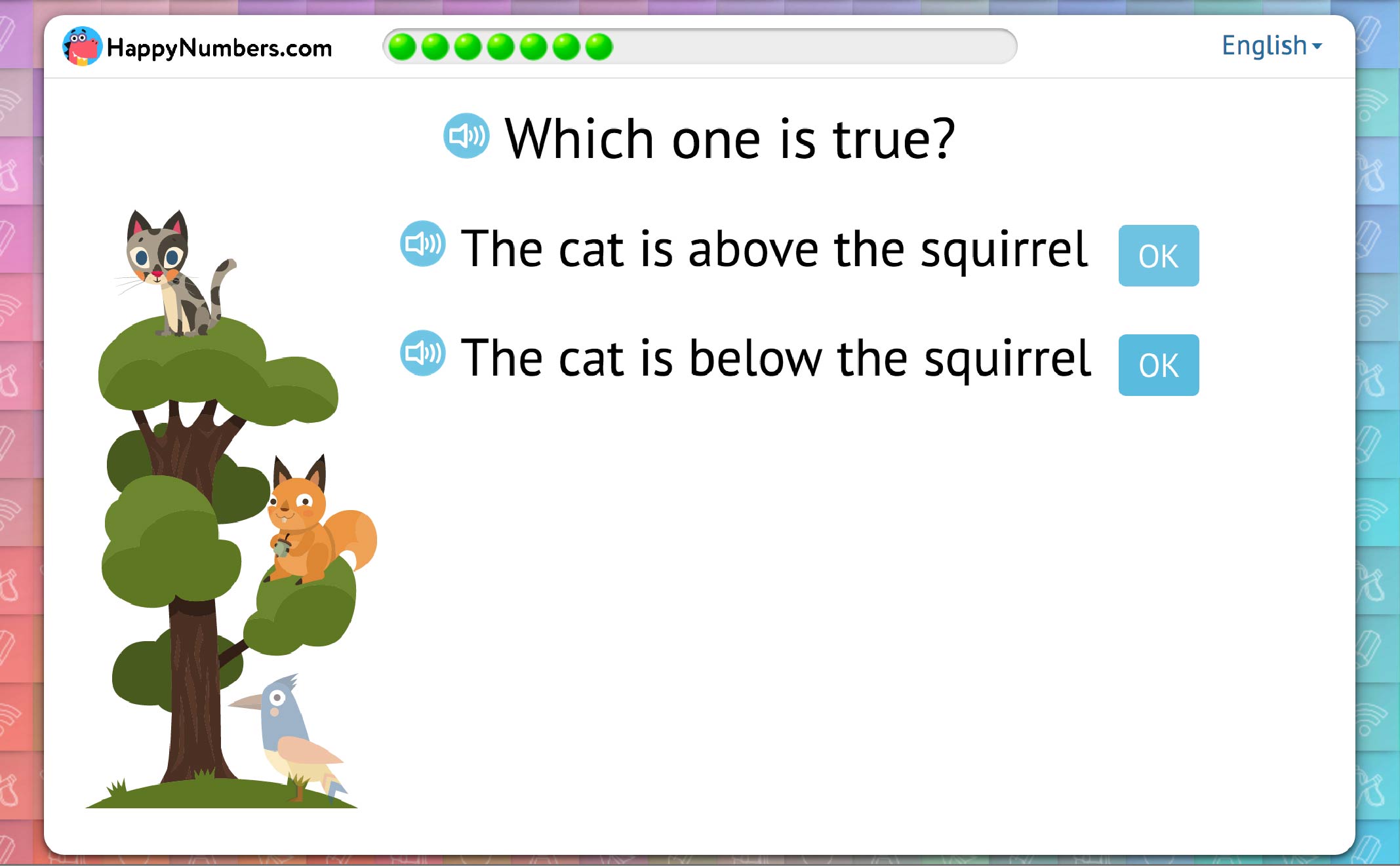
Finally, students can position objects based on the terms above and below:
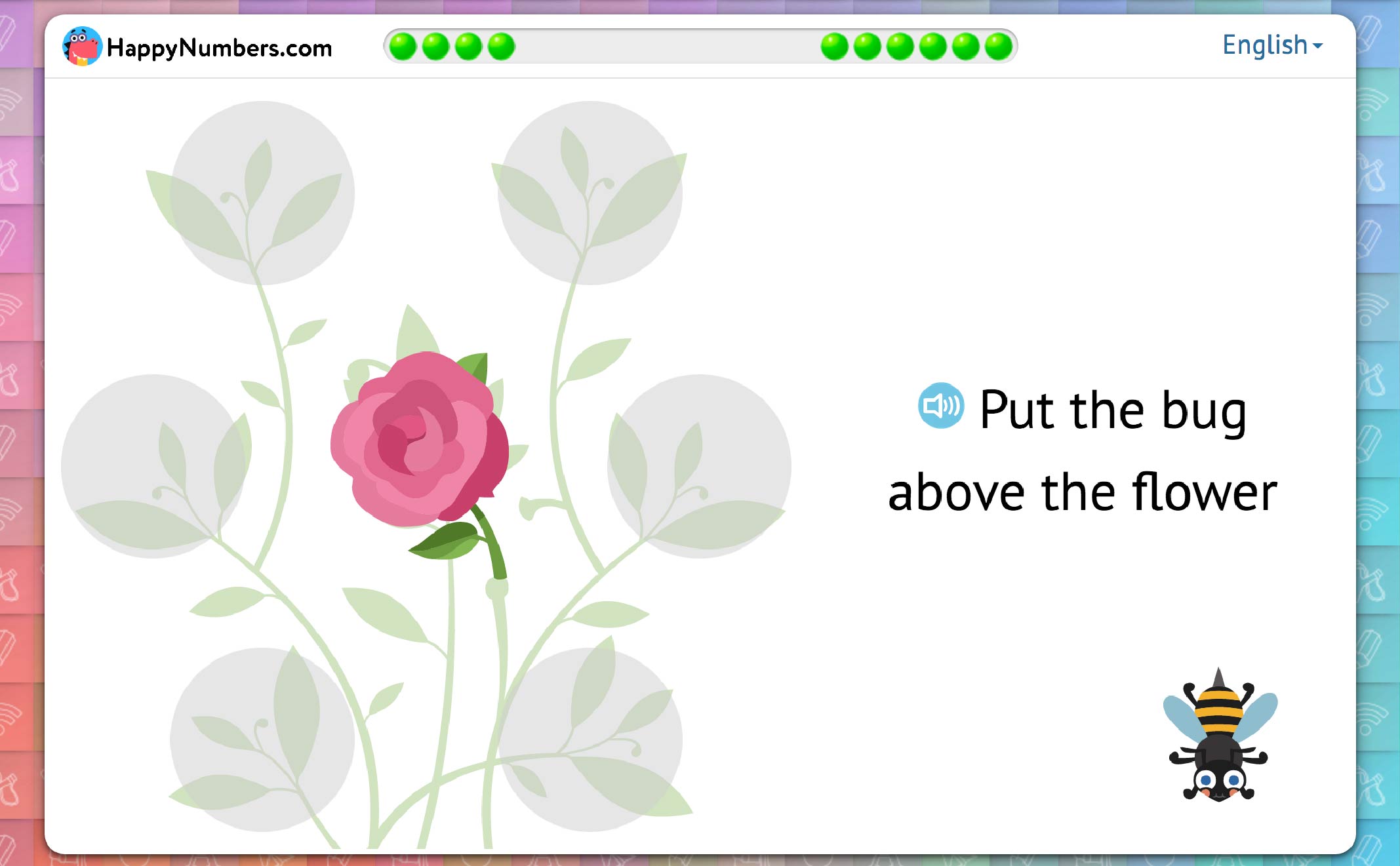
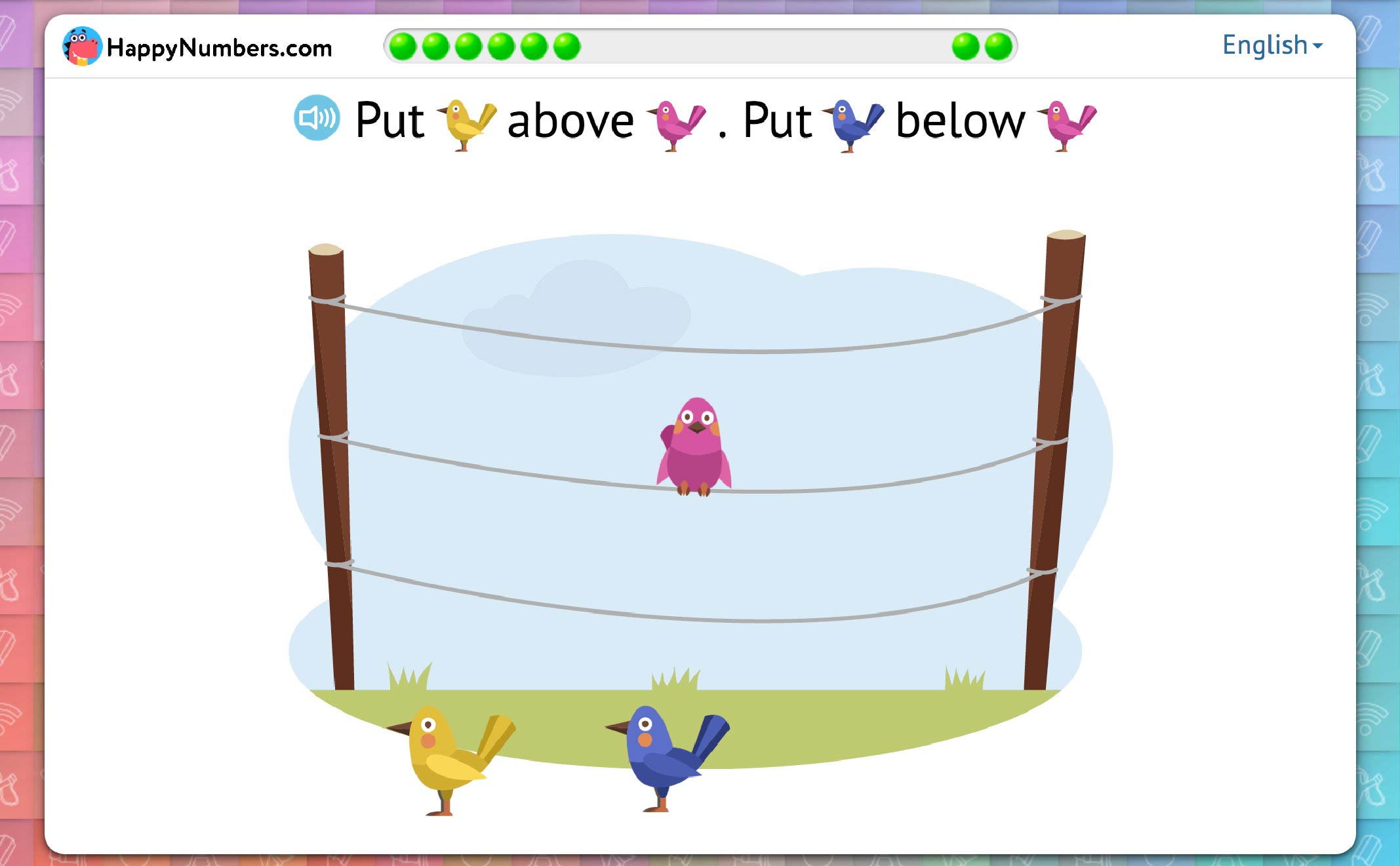
Similarly, the perspective in determining in front of/behind is also clearly implied in most cases. In two typical situations, students correctly assume the perspective without having to be told.
The first situation is when the student is an onlooker, for then the direction of his gaze is the forced perspective:
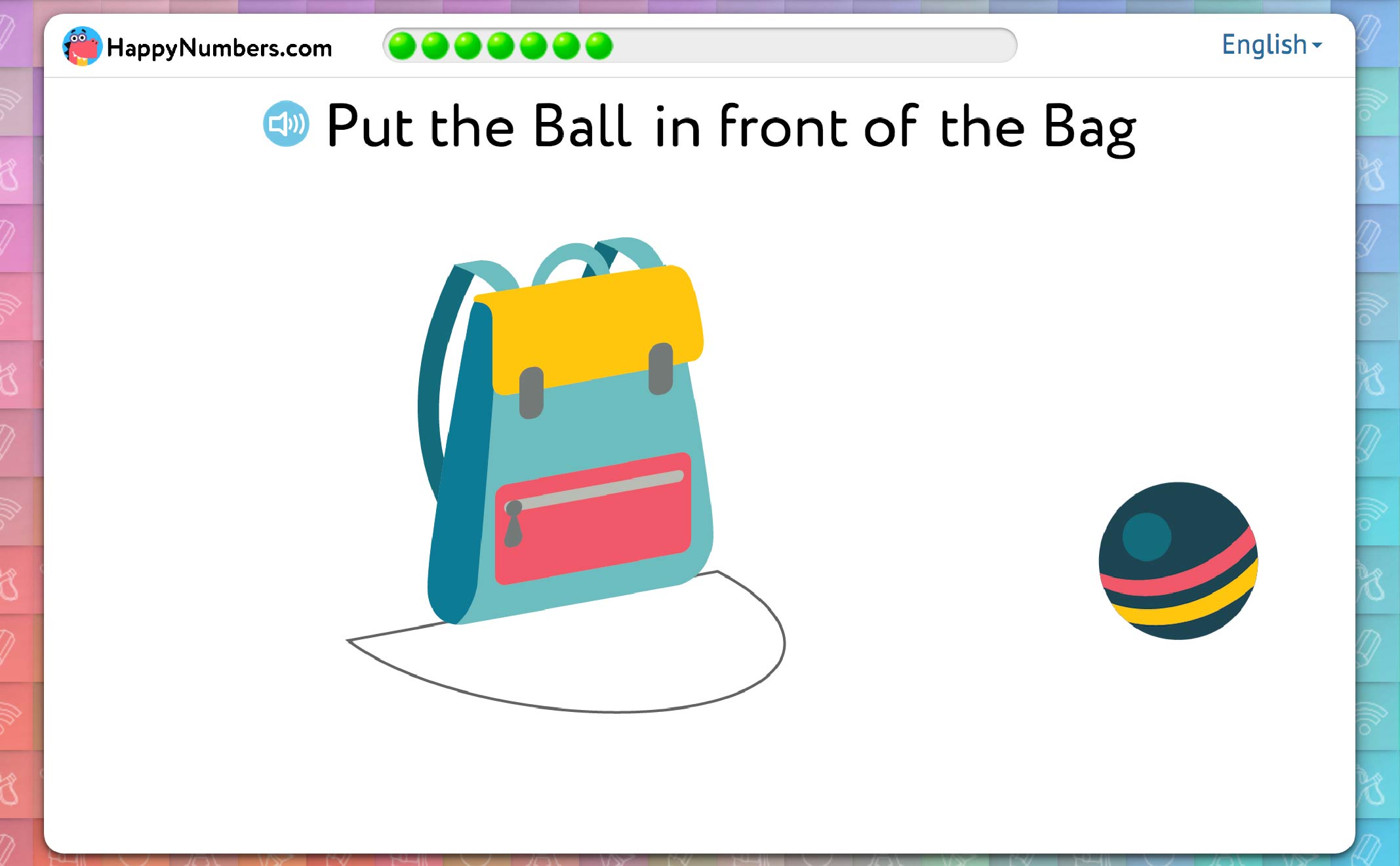
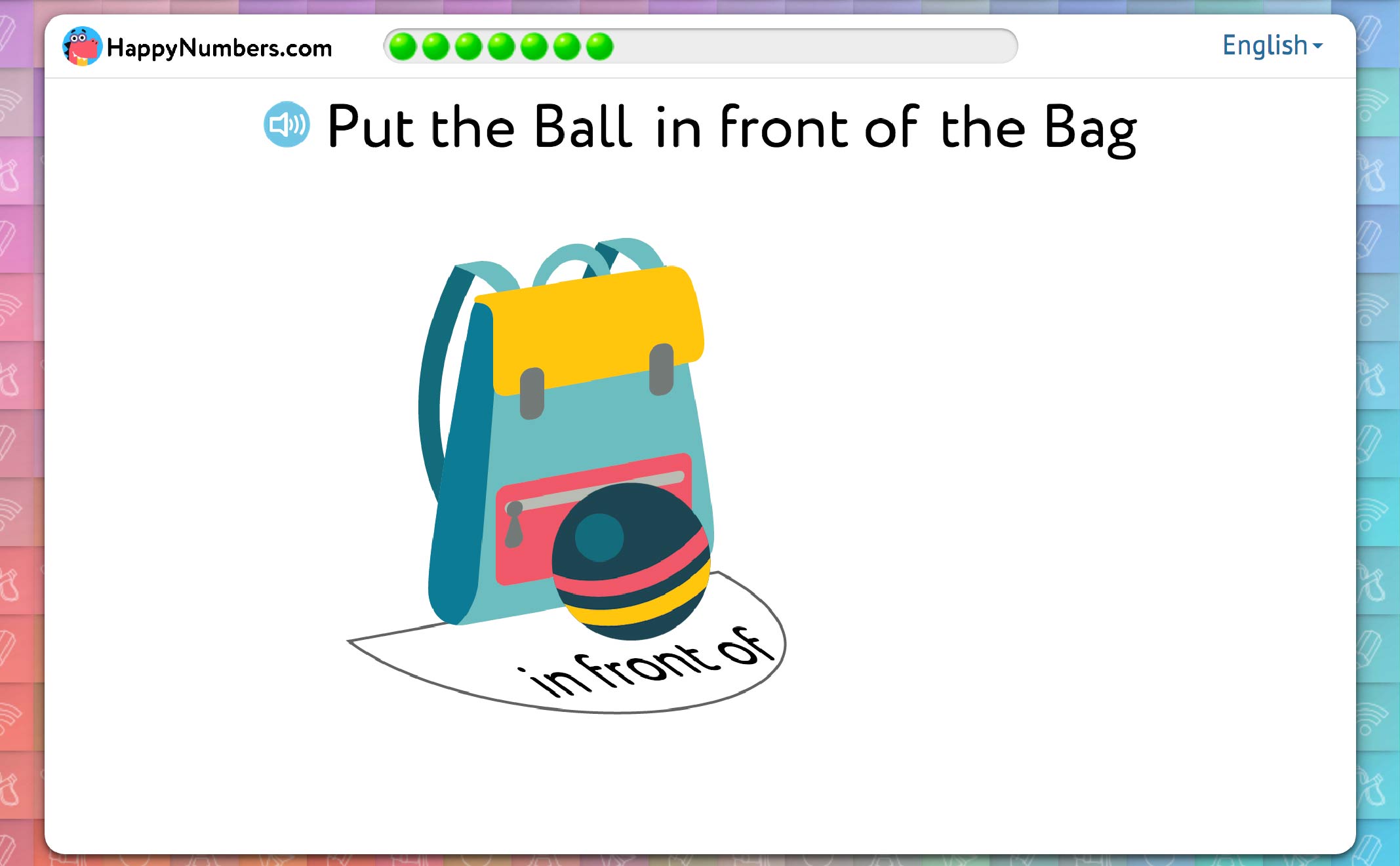
When looking at a picture or a computer monitor, there is usually little doubt as to “what is in front of what”.
The second situation is when there is motion:
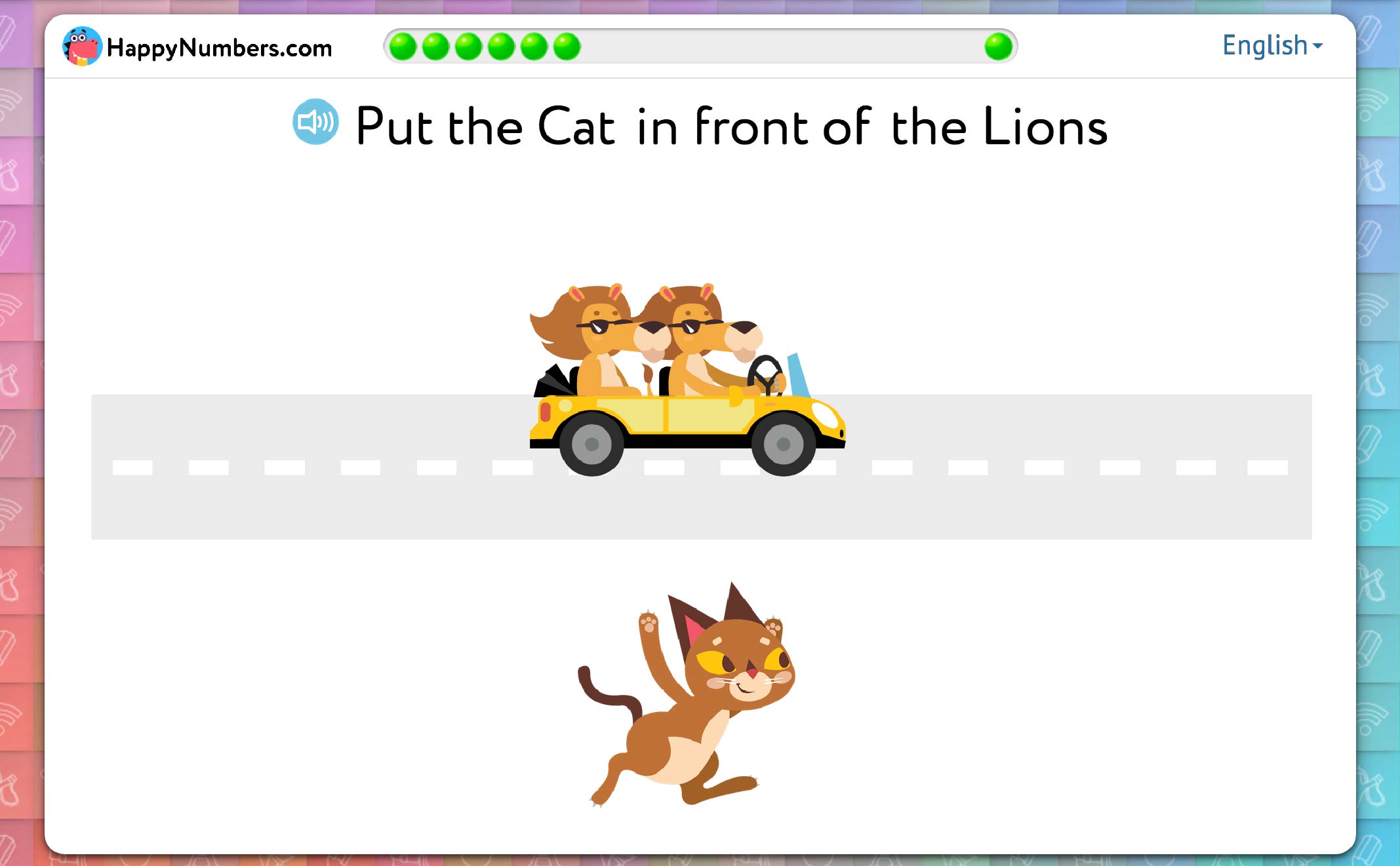
Then, the preference is toward the direction of movement:
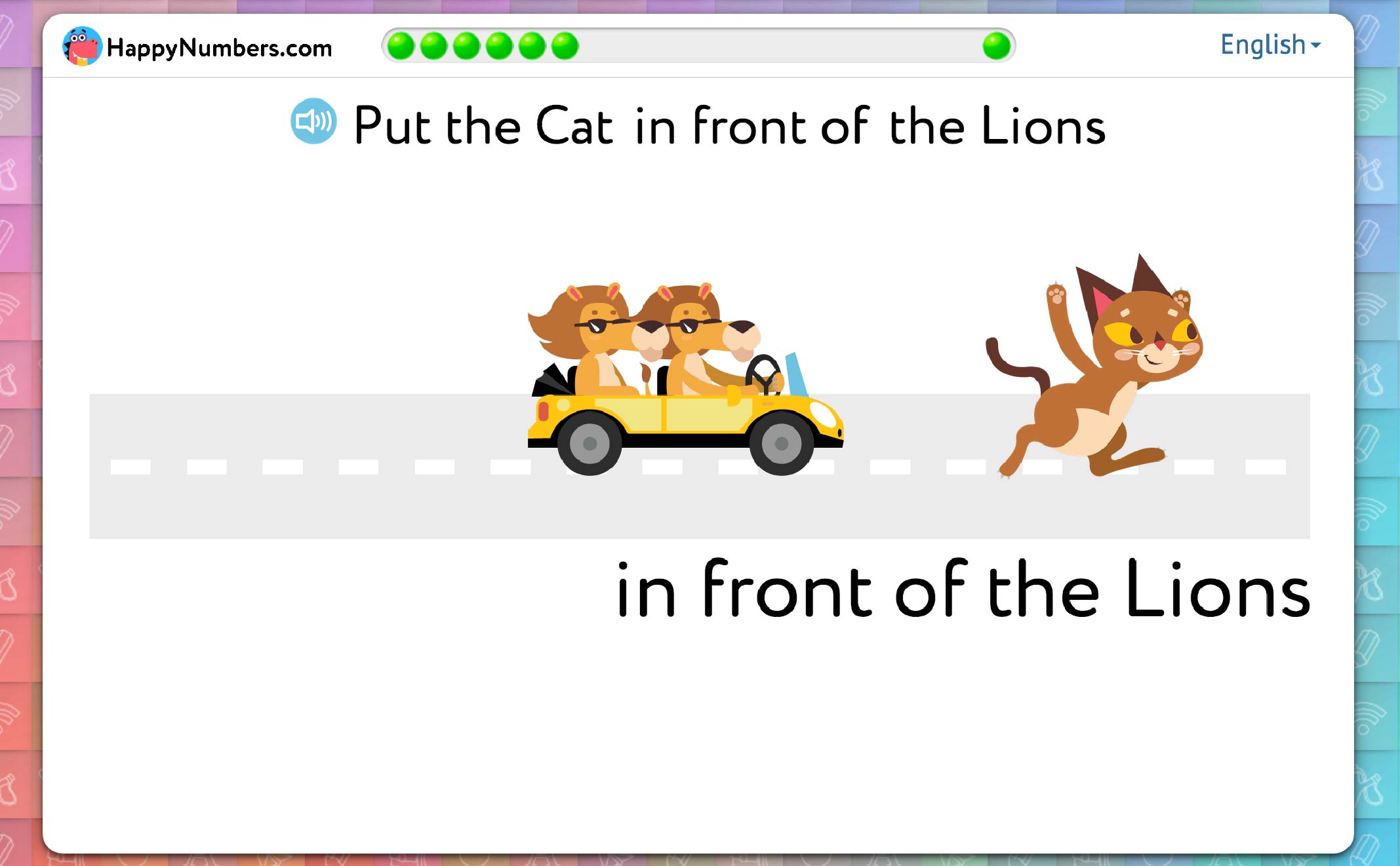
In this instance, students cannot choose in front of or behind based on their own position as an onlooker (since the lions and rabbit are situated in one plane perpendicular to the gaze). Rather, the forward motion causes the lions (in this case) to become the onlookers.
The relative positions left/right, on the other hand, have no implied perspective. As the perspective is more abstract or always changing, the concept of this relative position is much more difficult for children to grasp. Therefore, it is not addressed specifically as a grade-related standard.
Like learning to read an analog clock, understanding left and right is developmental in nature. When students’ minds are ready to grasp the abstract concept, they will reach mastery. Until then, teachers can provide them with repeated exposure to the concept and mastery of more concrete relative positions.
When it comes to relative positions, Happy Numbers focuses on helping students master above/below, in front of/behind, up/down, and beside/between. In addition, we have exercises that develop students’ comparison skills and language (i.e., smaller, longer, taller). Hop online and take a look 😉
Yours,
Evgeny and Happy Numbers Team
Evgeny and Happy Numbers Team
