Teaching Why (not just How): Column Addition and Subtraction
With enough rote practice, most students can learn to “carry the one” or “exchange/trade ten” to solve multi-digit addition and subtraction problems. But to truly understand the process and become fluent with it, students need to take a look under the hood and see the place value principles at work behind the operations. That’s why at Happy Numbers we focus on why the standard algorithm works, rather than how it works. We believe that by building understanding first, fluency will follow (and not vice versa). As a result, students are better able to find and correct errors and they are better-equipped to work with larger numbers and even decimals.
This post will share some of the exercises we suggest for building deep conceptual understanding of column addition and subtraction. We’ll also explain how we scaffold instruction to help students create meaning, rather than just memorize steps. All of the exercises shown are available at Happy Numbers, but you can re-create them in your classroom offline as well.
Prior knowledge
If you have students who aren’t quite ready for column addition and subtraction, see our discussion of Place Value and Teaching Addition and Subtraction to build foundational skills and understanding.
All of the exercises mentioned here are part of the HappyNumbers.com course and are presented along with exercises using other representations.
1. Begin with Place Value Reinforcement
We start by priming the pump of students’ place value understanding. Here, we present 2-digit addition problems with and without regrouping. The goal is to get students thinking of numbers in terms of their place value. Therefore, they first break each number into tens and ones:
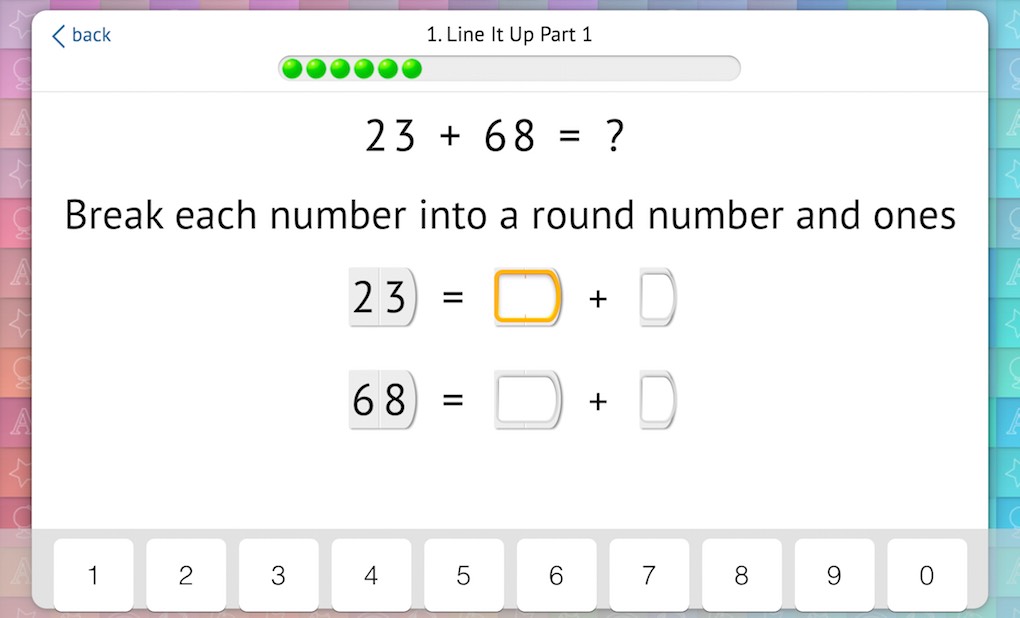
We’ve seen teachers make their own place value tools like these out of index cards or nesting cups:

Students then add the tens and ones separately. Finally, they reach a solution by adding a round number to a non-round number mentally. There’s no mention yet of “carrying” or exchanging. Students simply rely on knowledge they’ve built previously to complete the solution. Note that all equations are presented both horizontally and vertically.
We follow the same approach with subtraction, but begin exclusively with problems that don’t require exchanging. This allows students to become familiar with the components of the problem.
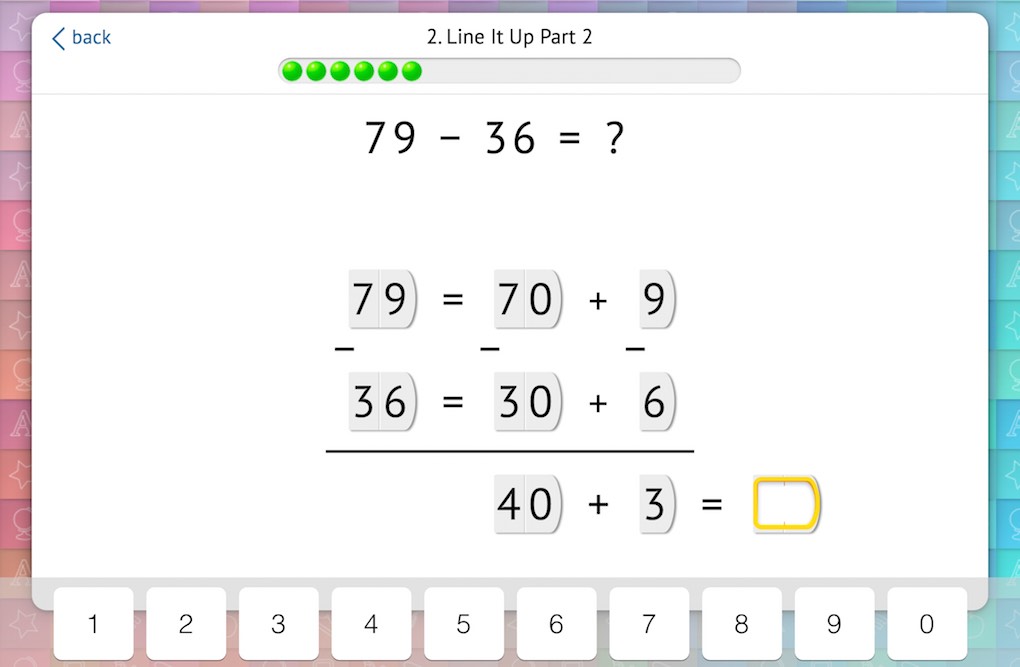
2. Introduce the Need to Exchange (and the Meaning Behind the Process)
Once students have mastered that preliminary step, we introduce the need to exchange the ten. Prompted by a question, students realize that they cannot subtract the ones:
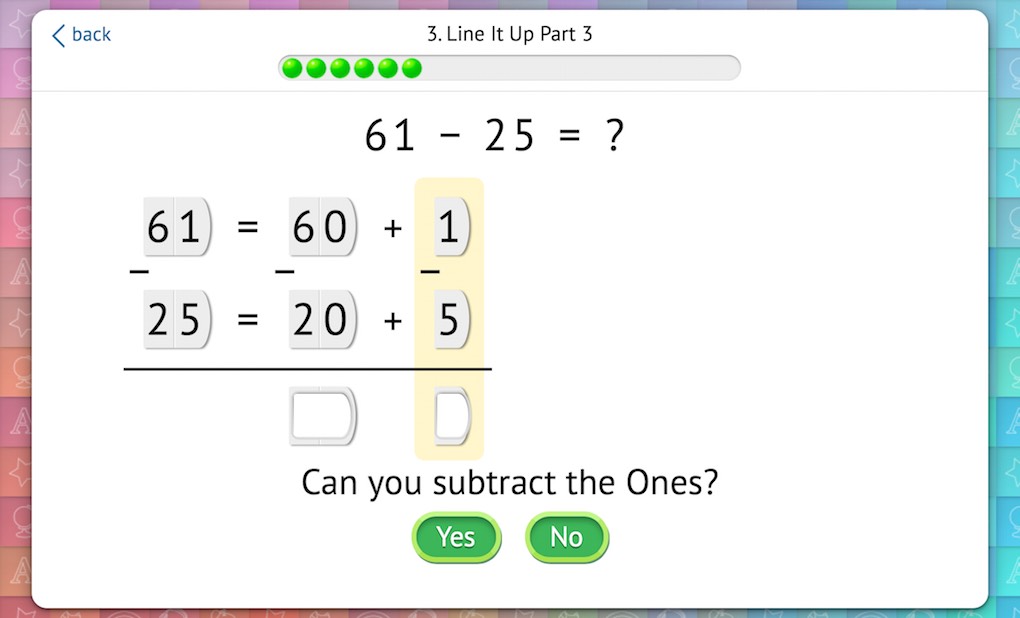
From there, we walk students through each step of the procedure, visually reinforcing what is happening and why:
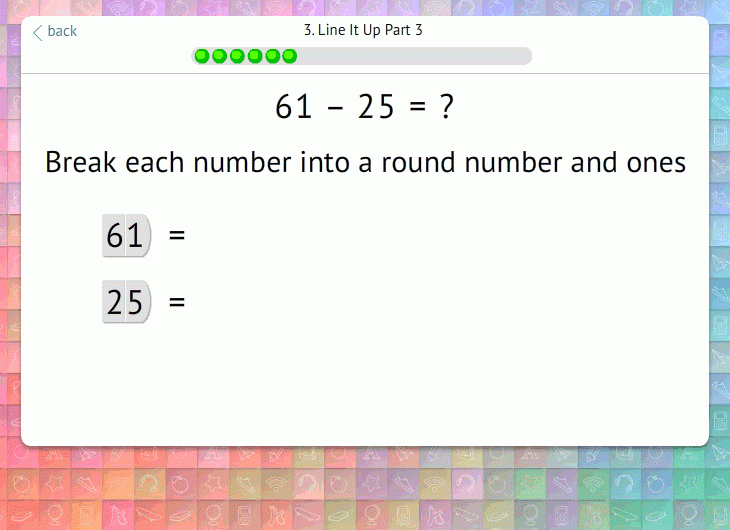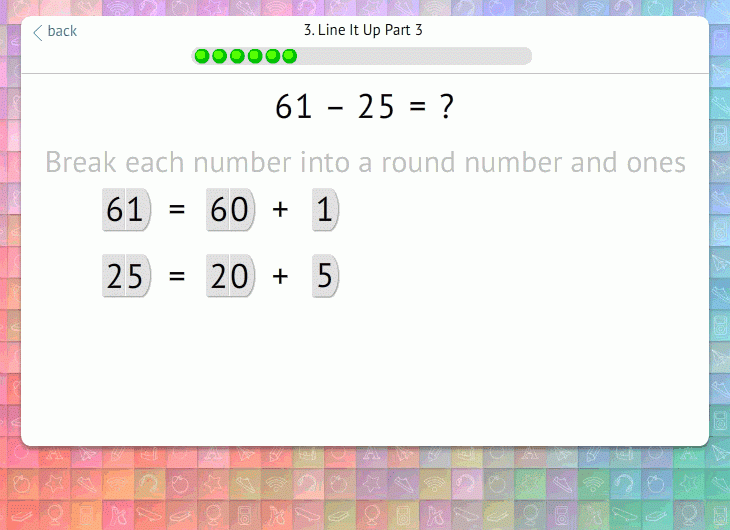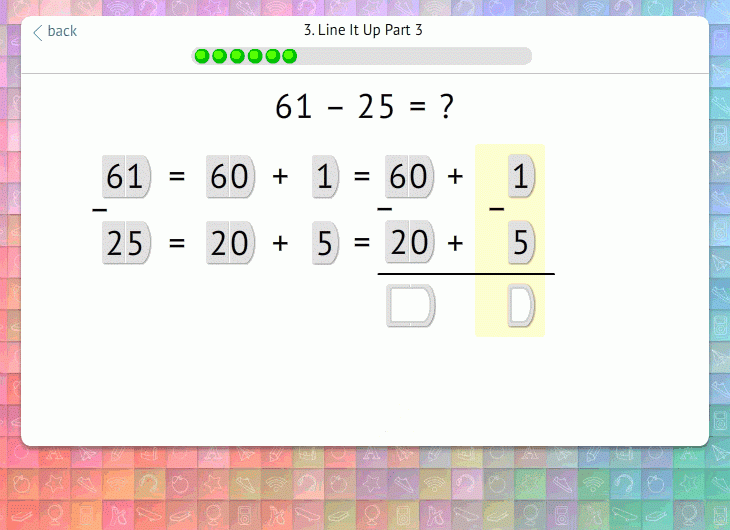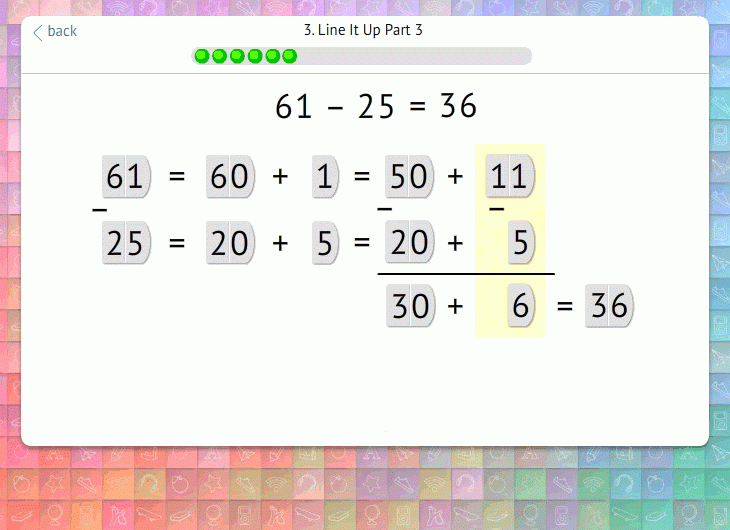
3. Fill In Conceptual Gaps
It might appear that students are now ready to jump into column addition and subtraction, but we’ve found a few intermediary skills that are important to isolate and master. Without them, students can run into trouble and not understand how to resolve it. One of these intermediary steps is to remove placeholder zeros, forcing students to rely on place value knowledge.
We introduce this skill first without regrouping. You’ll see that these activities look almost identical to the previous ones, but there are no placeholders:
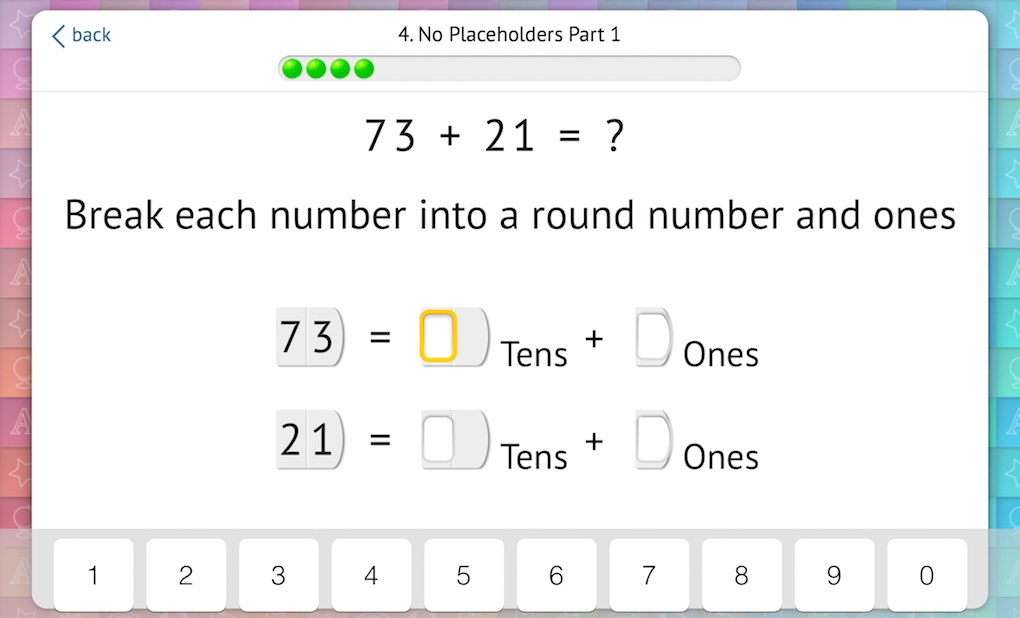

We then introduce equations that require regrouping. Here, Happy Numbers breaks apart the sum in the ones column and prompts students to move the ten to the tens column (carry over):
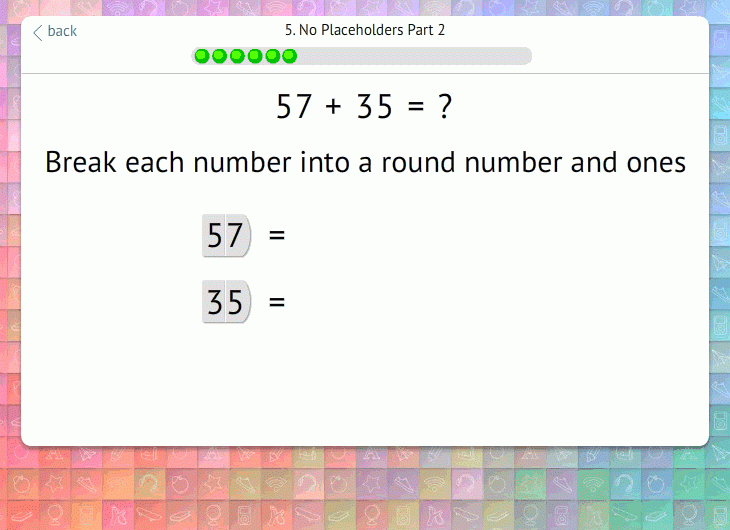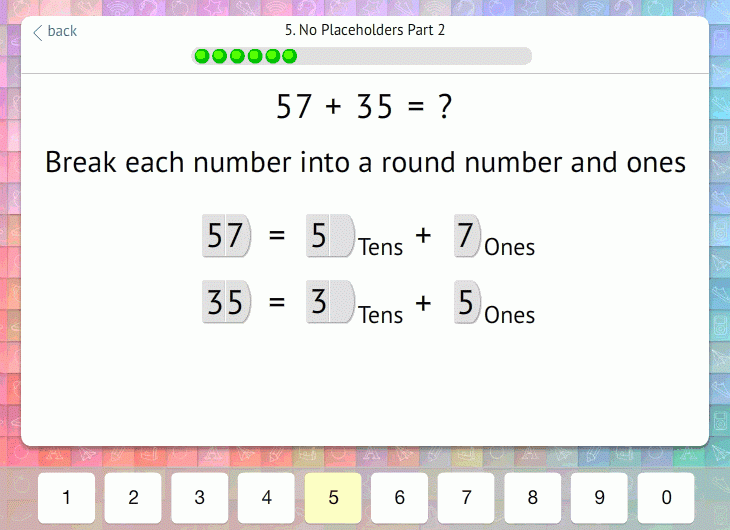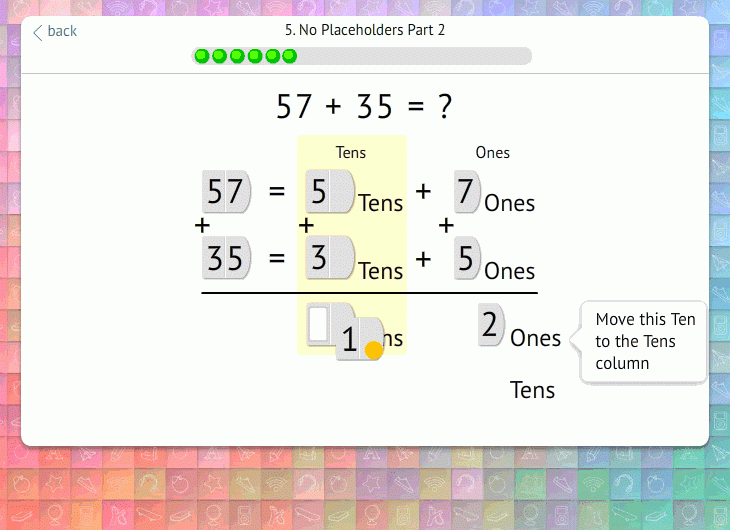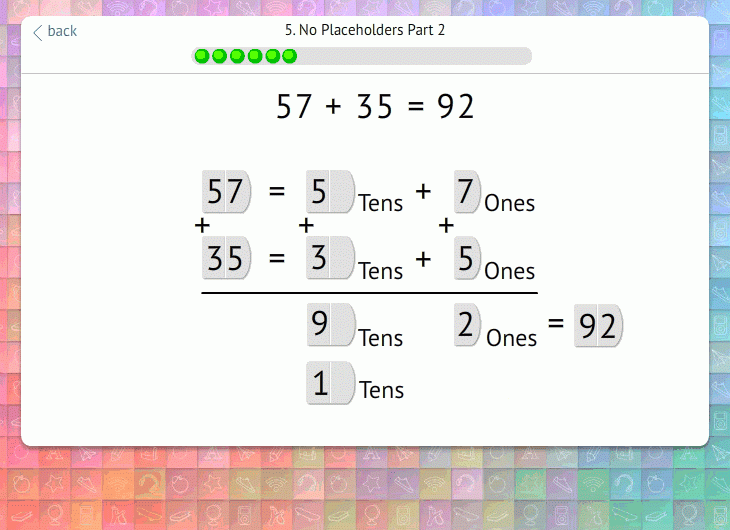
Again, we agree with most teachers that conceptual understanding is most important here. We don’t focus on where to put the 1; what matters is that students recognize its value and account for it in the total.
4. Put It All Together (with lots of support!)
Now that students have a feel for how to add without placeholder zeros, we introduce the step of deciding whether regrouping is necessary. Students are prompted to choose whether or not their sum in the ones columns will include tens. Their choice here determines the next step in solving the problem:
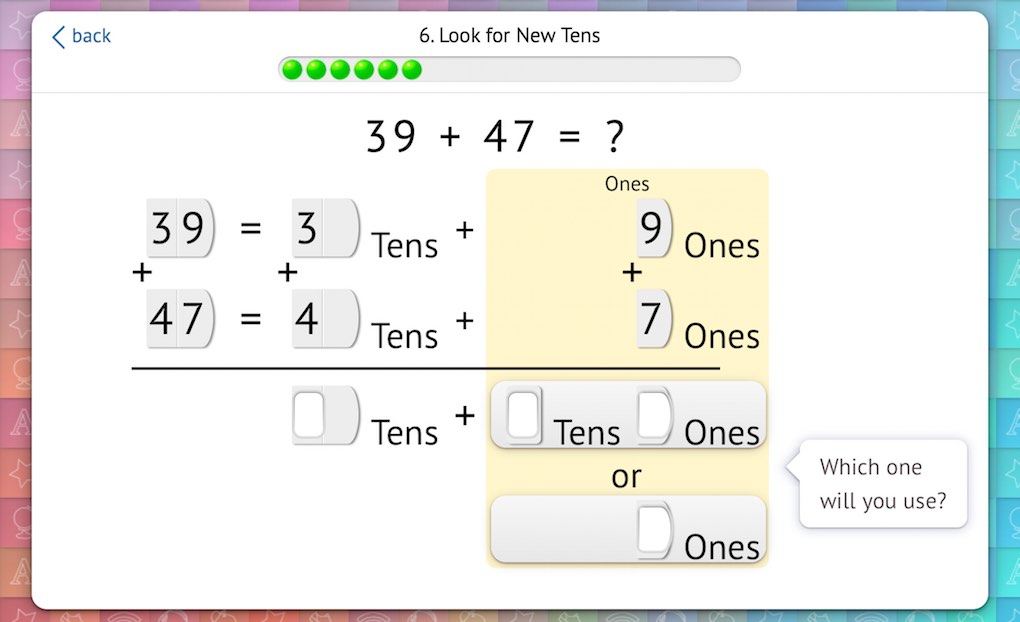
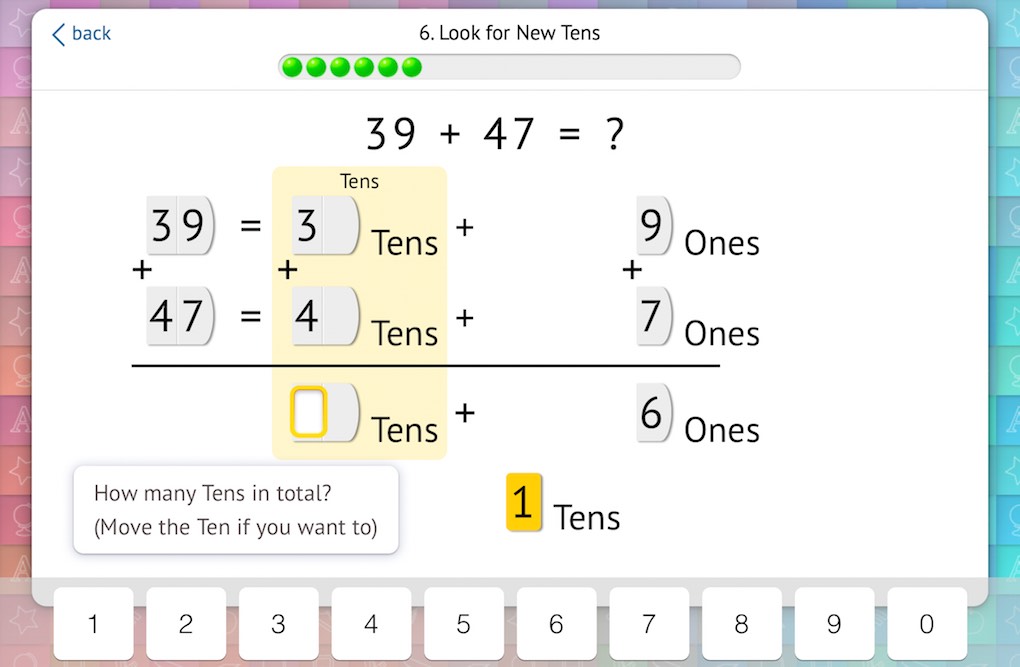
We also give students an option as to whether or not they need to visually carry the one to the tens column:
We use a similar approach to teaching subtraction with no placeholder zeros, relying on knowledge that has been built through previous activities. Again, we begin by using only problems that don’t require exchanging:
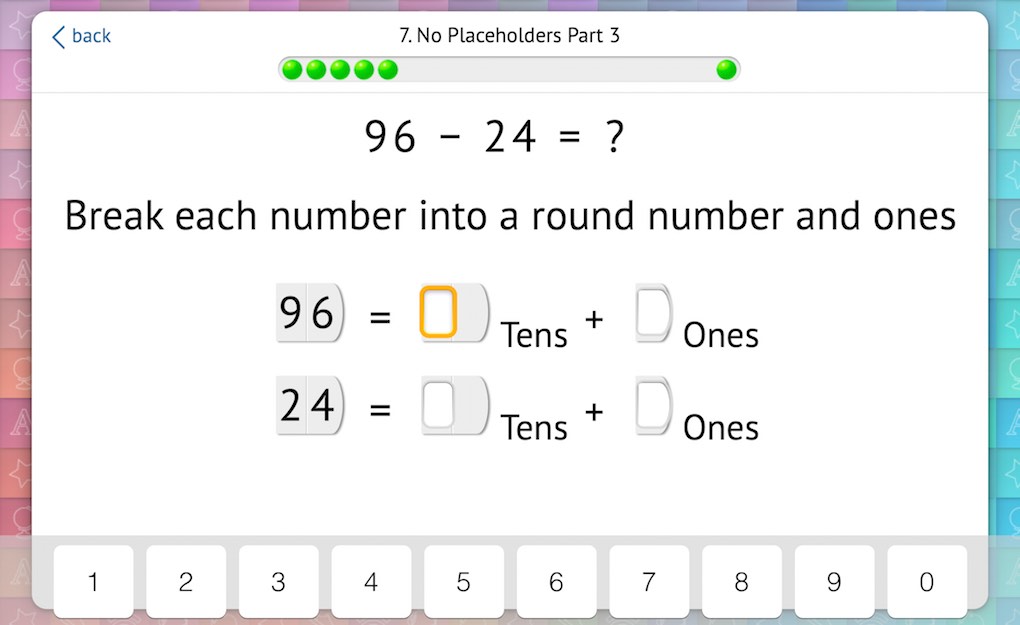
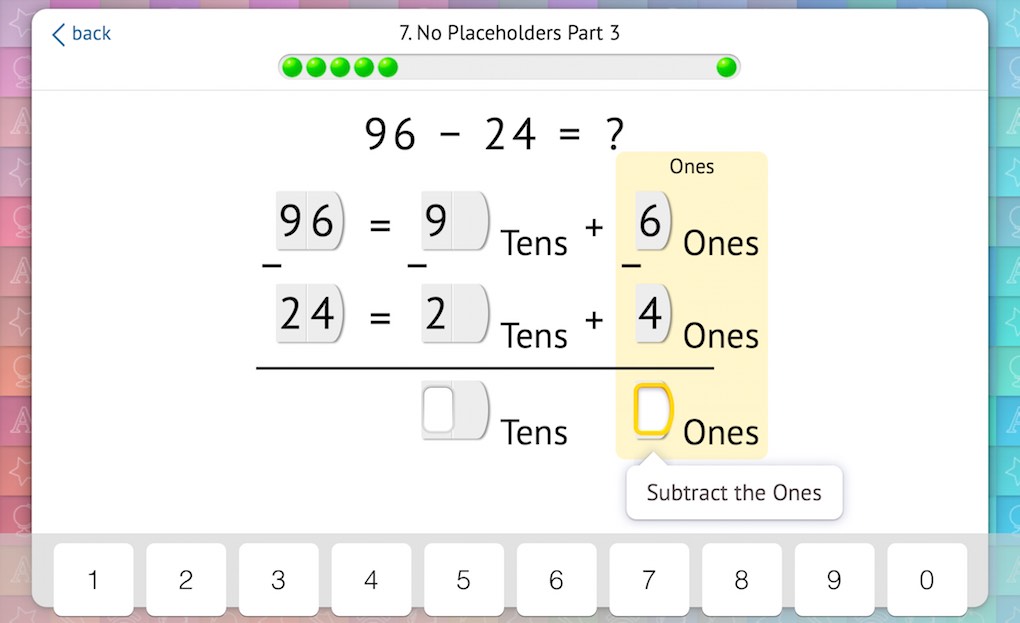
Finally, students perform column subtraction with exchanging (if needed) with full understanding of the meaning behind the procedure:

As you can see, there’s no “smoke and mirrors” in this approach to teaching column addition and subtraction. Right from the start, students understand why each step in the procedure is needed and where the numbers are coming from.
Happy Numbers’ technology allows us to present these concepts in an interactive way that pencil and paper just can’t match. However, it’s still important to translate these skills to traditional classroom tasks.
—
Happy teaching!
Evgeny & Happy Numbers Team
Happy teaching!
Evgeny & Happy Numbers Team
