The Relationship between Multiplication and Division

Mathematics is a very logical science, built on rules, principles, and relationships. Mathematical thinking is based on the sequential study of procedures, first with concrete objects, then with visual models, and only then with abstract symbols and concepts. This systematic approach to learning allows students to grasp the meaning of mathematical operations and the connection between them.

From Grade 3, Happy Numbers gives step-by-step explanations of multiplication and division, their connection to addition and subtraction that students mastered earlier, and how to apply these operations. In addition, students learn the connection between multiplication and division, since these operations are inverse to each other. Subsequently, they strengthen and develop this knowledge on various tasks. This article examines how Happy Numbers helps students explore the relationship between multiplication and division, so they can fluently perform these operations.

 

The easiest way to establish a relationship between multiplication and division on an intuitive level is through the array model, which equally suits both operations. Happy Numbers provides a series of exercises that lead students to conceptual understanding of this relationship.

The first exercise has students match multiplication and division facts that correspond to the same array model. Each of the three tasks starts with division. For example, the screenshot below shows the third array, while results of the first two are saved in the upper right corner:

 

 

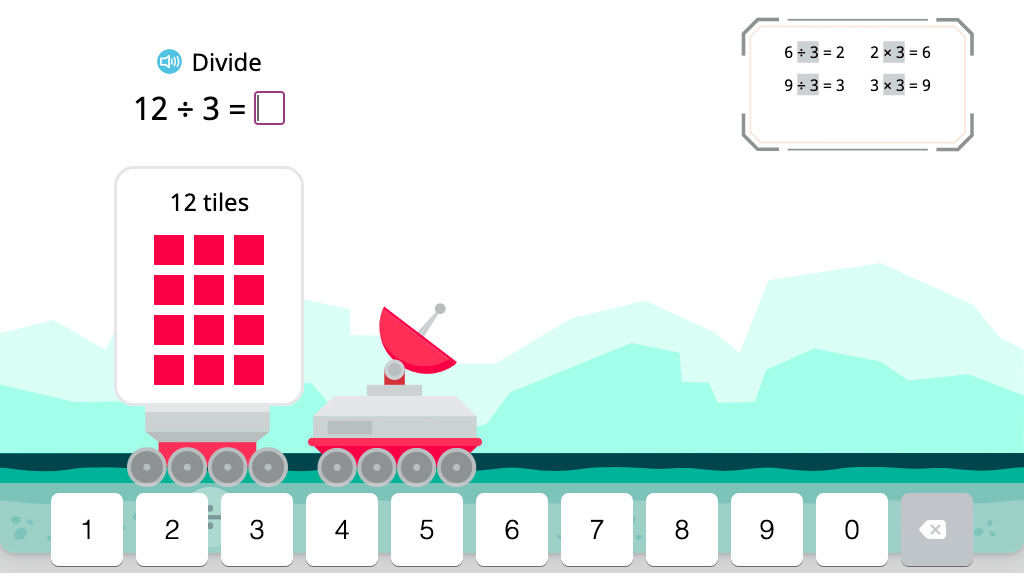
If students respond incorrectly, the following hint reminds them of an interpretation of division that allows them to find the answer:

 

 

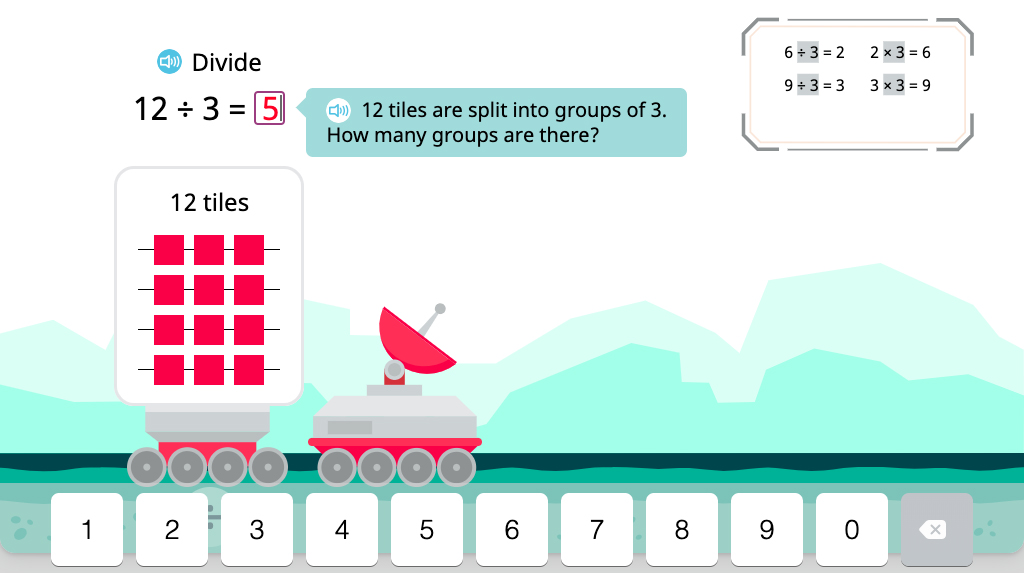
The next step is completing a multiplication sentence based on the same array representation:

 

 

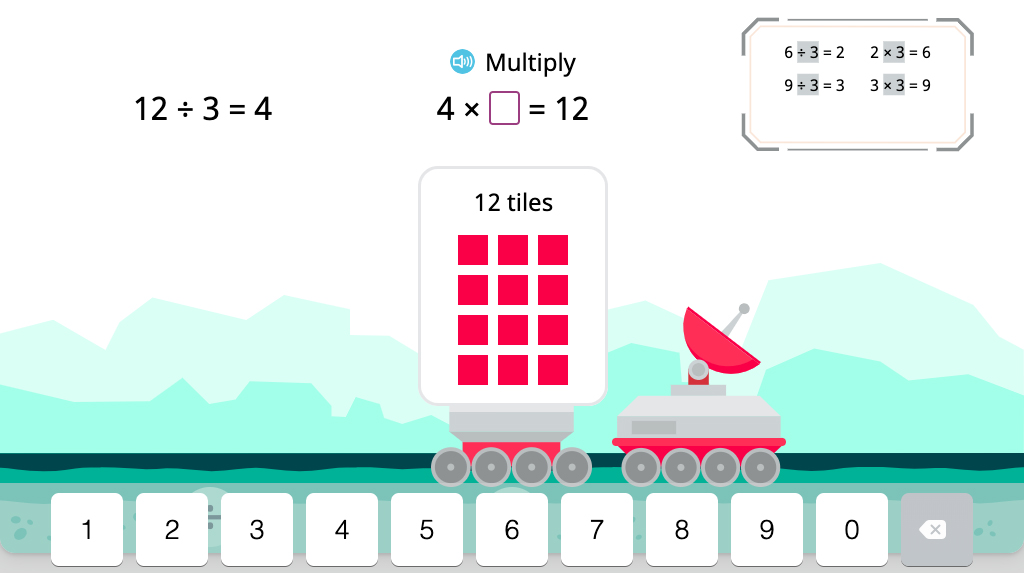
Now, students look at the results of the three tasks and come to an important conjecture:

 

To see the full exercise, follow this link.

Division by 3 is related to multiplication by 3. Not only that, but the relationship is true for any number: Division by a number is related to multiplication by the same number.

This makes the statement “Division is related to multiplication” more specific, and it can be further detailed to become an immediately usable tool.

Related Multiplication and Division Facts Are Composed of the Related by Same Numbers

To detail the relationship established above, Happy Numbers provides exercises that attract students’ attention to numbers involved in the two operations (division and multiplication) corresponding the same array model:

 

 

Students highlight three pairs of numbers, and this color-coding helps to compose a statement:

 

 

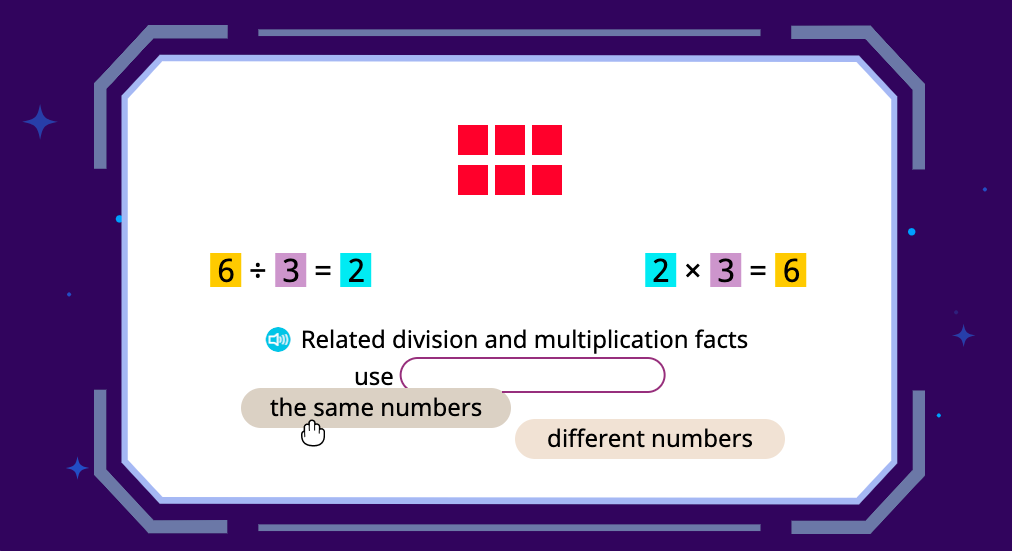
This statement then allows students to complete multiplication facts related to the given division fact. For example:

 

 

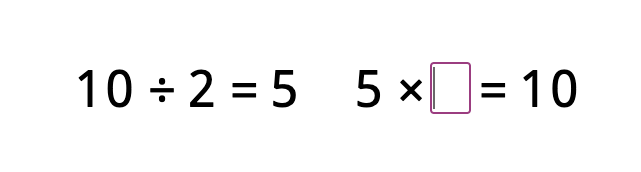
In case the answer is incorrect, students get the following reminder:

 

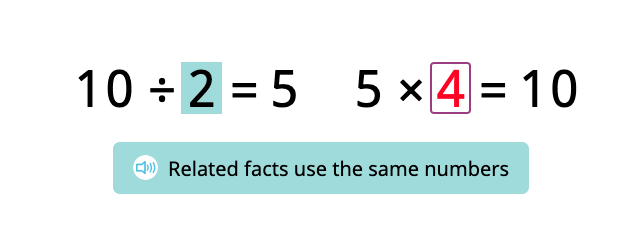
These tasks use a single blank however, the placement of the blank varies. It can be in either equation and in any position. To see the full exercise, follow this link.

 

Thus, students grasp that both of the related equations are made up of the same numbers. This adds an important detail to the previously established relationship, and together they describe a very practical fact:

 

Division by a number is related to multiplication by the same number.
The two related equations are made up of the very same numbers.
Example: 14 ÷ 2 = 7, 7 × 2 = 14

 

This detailed description of the relationship between multiplication and division allows students to compose a division equation related to a given multiplication equation, and vice versa.

 

To get used to the relationship, students work on straightforward tasks within 100: for a given division equation, they find the related multiplication equation in the times table.

 

This is done in two steps. The answer to first part of the task…

 

 

…allows students to limit the search of related multiplication facts to a times table for one number (2 in this example).

 

 

In the above activities, students don’t perform multiplication or division; instead, they develop the mathematical thinking to discover the relationship between these types of facts, which will help them solve problems in future activities.

 

Dividing within 100 Based on the Relationship between Multiplication and Division

 

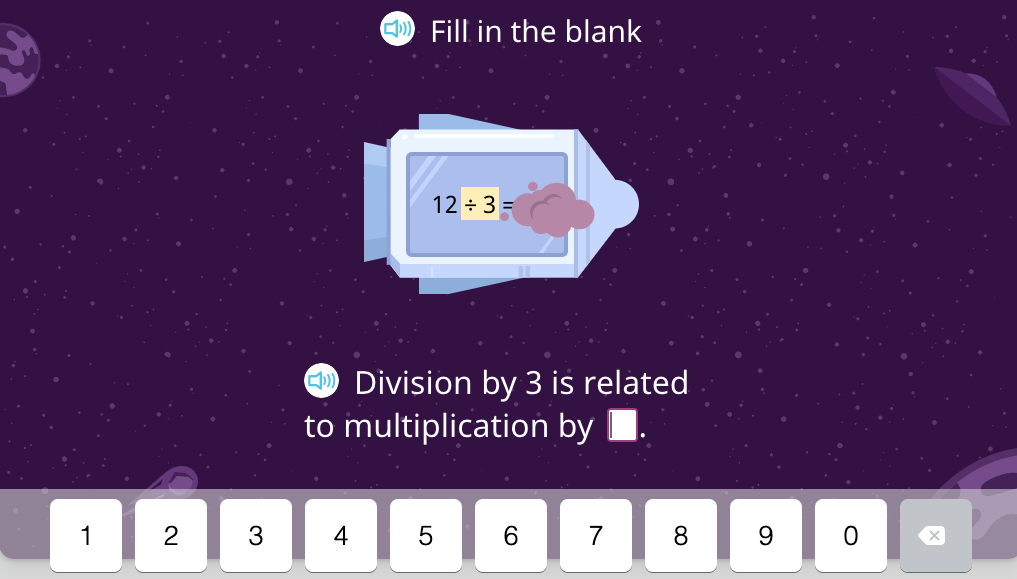
By now, students have looked only for a multiplication fact related to a given division fact, and it’s time to consider a more practical case when the result of division is unknown.
Happy Numbers introduces this task so that it looks very similar to the previous task with a given division fact. This helps students realize that the relationship between multiplication and division remains applicable here:

 

 

…and the related multiplication fact can be found in the corresponding times table (×3 in this example):

 

 

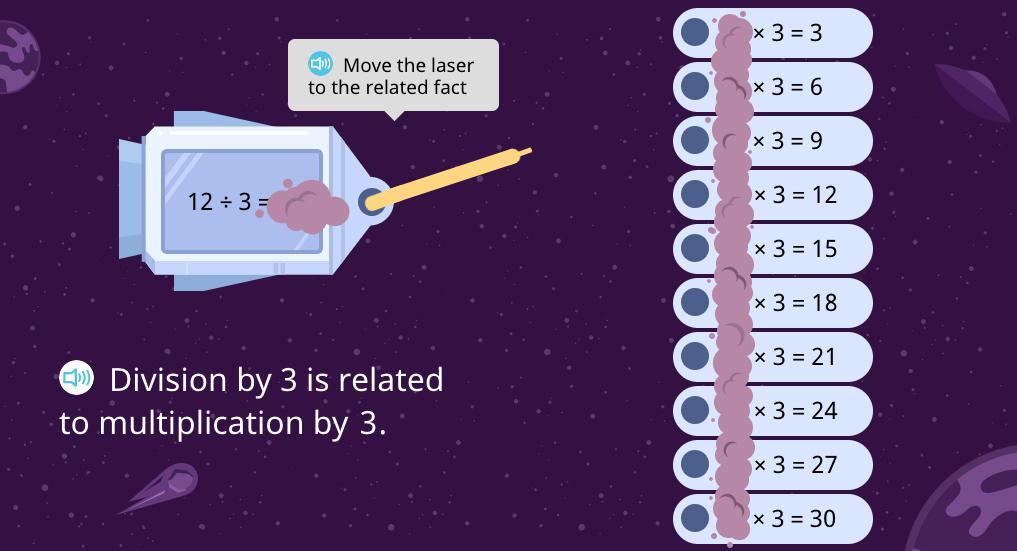
There is an important hint for those who need it:

 

 

In the above screenshot, the other factors in times 3 table are hidden to emphasize that the related multiplication sentence is identifiable without any information about this factor.

So, the related sentences are:

 

 

Here, the division result and one of the factors are actually the same number, so knowing one of them means knowing the other, too:

 

 

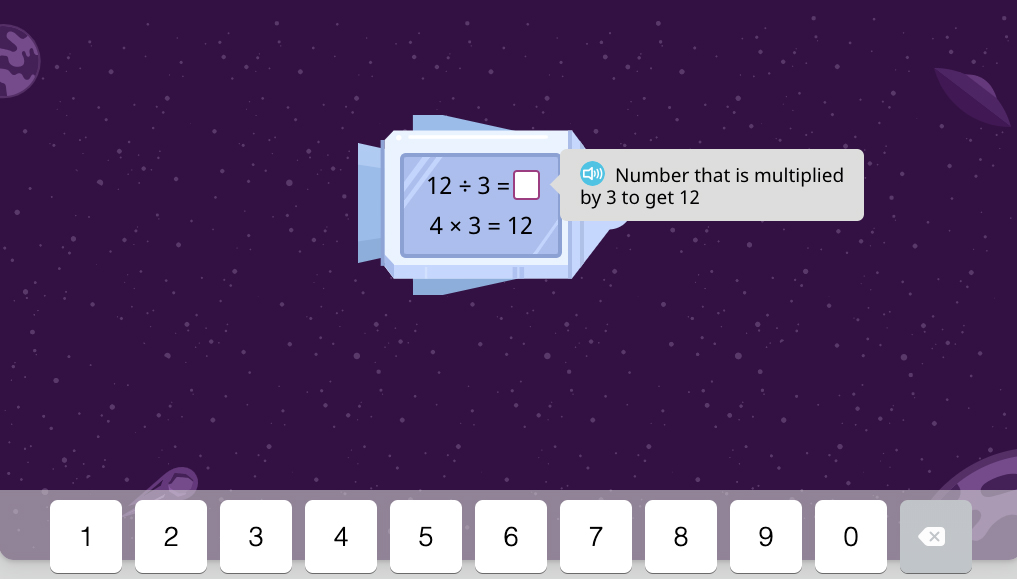
Knowing the basic multiplication fact 4 × 3 = 12 immediately implies that 12 ÷ 3 is 4.

To see the full exercise, follow this link.

The same strategy works for finding division facts related to basic multiplication facts (that is, multiplication of two single-digit numbers). Consider, for example, multiplication and division by 7. In the Happy Numbers curriculum, students work first on the ×7 multiplication facts and then apply the relationship between division and multiplication to divide. At this point, a hint reminds them of the relationship between multiplication and division:

 

In case of an incorrect answer, further support is provided:

 

 

Students receive yet more support if needed: the ×7 table can be made available by clicking the help button.

 

 

A double goal is achieved here: mastering the basic facts and grasping the relationship between multiplication and division.

 

Two Pairs of Related Multiplication and Division Facts

 

To further develop students’ understanding of this relationship, Happy Numbers introduces a multiplication fact, such as 3 × 8 = 24, and shows how the relationship between multiplication and division results in the division fact 24 ÷ 8 = 3.

 

It’s worth mentioning that there is another pair of related facts made of the same three numbers. This is due to the commutative property of multiplication: the multiplication facts in the two pairs just have their factors swapped. For example:

3×8 = 24

8×3 = 24

Each of the multiplication equations has its own related division fact.

 

 

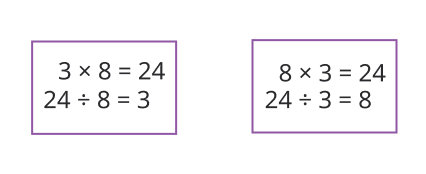
These fact pairs represent inverse operations: one, multiplying by 8 and dividing by 8, the other, multiplying by 3 and dividing by 3. So, relationships within each pair are very close, while all four of facts are related. Students learn that the divisor in the division fact and one of the factors in the multiplication fact are the same. In addition to that, both equations are made of the same three numbers.

 

 

Interpretations and Definition of Division

 

In elementary school, division is normally introduced by considering its two interpretations: finding the number of groups and finding the number of objects in each group. Both of them use equal sharing of objects between several groups while each interpretation addresses a different question.

 

Let’s start with interpretation of division as finding the number of groups when the number of objects in each group and the total are given. Consider, for example, this task from the Happy Numbers curriculum:

 

 

The number of groups (boxes) can be found by division 10 ÷ 2 = ▢. At the same time, the task can be represented and solved as equation for the unknown number of groups: ▢ × 2 = 10.

 

Another interpretation of division is finding the number of objects in each group when the total and number of groups are given. For example:

 

 

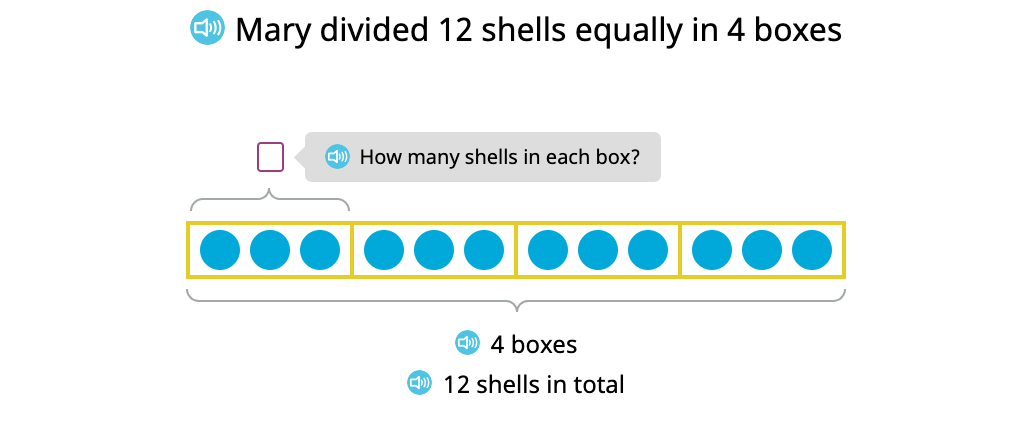
Like the previous example, the unknown number can be found either way: by division 12 ÷ 4 = ▢, or by solving an equation for the unknown number of objects in each group: 4 × ▢ = 12. Due to the commutative property of multiplication, the factors can be swapped so that the unknown factor is in the first position ▢ × 4 = 12, as with the first interpretation.

 

Thus, in both interpretations, the unknown can be found by solving an equation in the same form:

▢ × divisor = dividend

despite the different meanings of the unknown (the number of groups or number of objects in each group). So, it does not matter which of the two interpretations is used. For example, 120 ÷ 8: both imply the same equation ▢ × 8 = 120 for finding the quotient. The two interpretations of division are consistent!

 

The fact is that finding an unknown factor is actually the definition of division. More precisely:

 

– Division is finding the unknown factor from the equation ▢ × divisor = dividend

or in other words:

– The result of division is a number that is multiplied by the divisor to get the dividend.

 

First of all, this implies that any known multiplication fact yields a division fact. For example, knowing that 25 × 6 = 150, one knows that 150 ÷ 6 = 25. This source of division facts is very useful until students master the standard algorithm for division. Actually, we used this strategy earlier to establish division facts corresponding to basic multiplication facts within 100.

 

Most important in understanding division as finding an unknown factor is that it covers all cases of division of real numbers, including the division of any whole number even when it does not result in a whole number quotient.

 

A Fraction as the Result of Dividing Whole Numbers

 

It’s not always possible to divide whole numbers and get a whole number result (division with a remainder results in a pair of whole numbers, not in a single number). So, the set of whole numbers and operation of division are extended to make it possible. Fractions come into play, and the equal sharing interpretation of division illustrates that the result of division could be a fraction. For example, in a task from the Happy Numbers curriculum, students divide 3 pastries equally among 4 plates

 

 

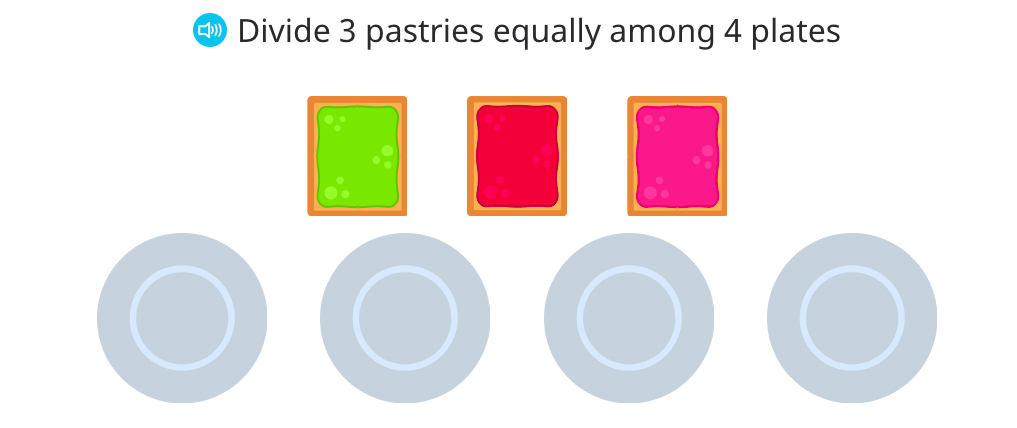
They work interactively with all needed support to arrive at the following result:

 

 

Completing a number of similar tasks leads students to reasonable conclusion that:

 

The result of dividing a whole number dividend by a whole number divisor is the fraction

 

 

It’s easy to come to this conclusion from understanding division as finding an unknown factor. Let’s check, for example, that 5 divided by 9 is equal 5⁄9. In terms of finding an unknown factor, that means: verify that 5⁄9 satisfies the equation

▢ × 9 = 5

which is true: 5⁄9 × 9 = 5.

 

Multiplication and Division as Inverse Operations

 

It’s often said that multiplication and division are inverse operations, but what does that mean exactly? Actually, it boils down to a useful statement which is just another way to express the relationship between multiplication and division as discussed above.

 

Let’s consider, for example, division of a number m by 7. The relationship between multiplication and division says that multiplying the result m ÷ 7 by the divisor gives the dividend m:

(m ÷ 7) × 7 = m

So, if a number is divided by 7, multiplying the quotient by 7 undoes division by 7, or for short: multiplication by 7 is the inverse operation for division by 7. This is actually true for any number n ≠ 0 in place of the 7:

Multiplication by n undoes division by n (n ≠ 0)

Vice versa is also true:

Division by n undoes multiplication by n (n ≠ 0)

These statements are pretty intuitive and helpful. For example, multiplication by 10 (or more, generally by an appropriate power of 10) with subsequent division simplifies multiplication of a decimal to multiplication of a whole number:

 

 

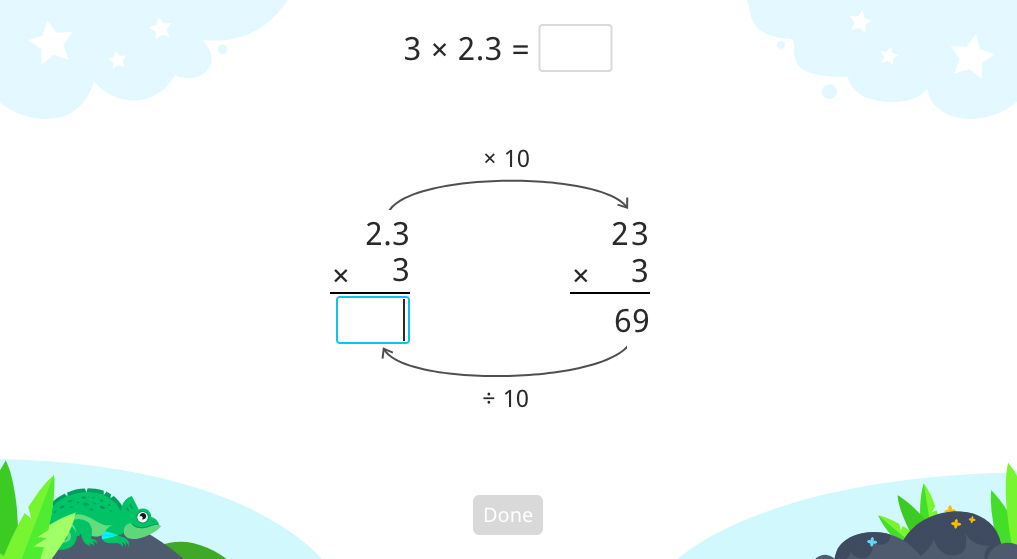
Starting with the original expression 3 × 2.3, students transformed it by multiplying the decimal factor by 10. This also means that the product is multiplied by 10, due to the associative property. Now, students divide by 10 in order to undo the multiplication and thus get the required original product.

 

This strategy also applies to multiplication and division of two decimal numbers.

 

Checking Division with Multiplication

 

It’s an activity with a double goal. The first goal is, of course, checking a calculation – important in particular when the division is “complicated” or when introducing new applications. It’s pretty “complicated” if, for example, long division looks like this:

 

 

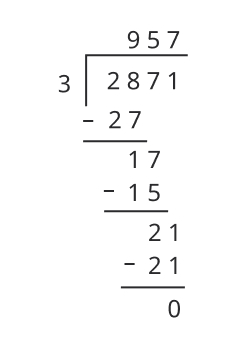
The solution can be verified by checking whether 957 × 3 = 2,871 is true.

 

An example of a new application of division is introducing division of a fraction by a whole number.

 

 

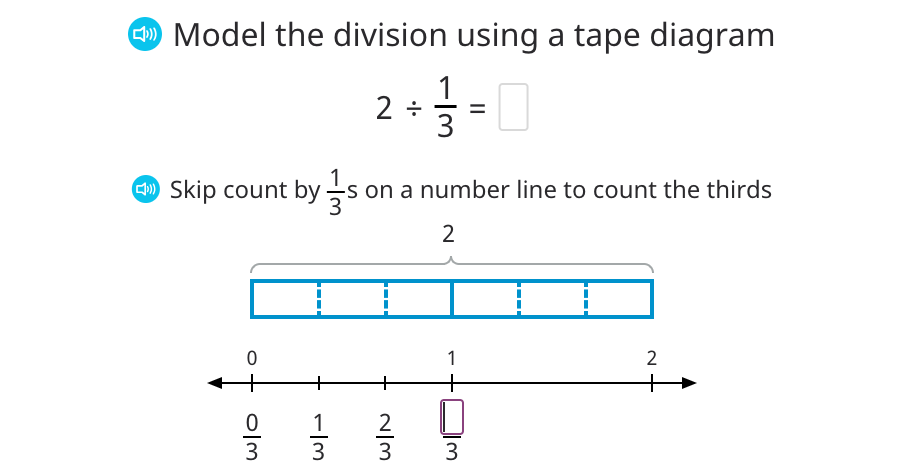
Verifying the result 2 ÷ 1⁄3 = 6 by checking if 6 × 1⁄3 = 2 is true is important here to reinforce conceptual understanding of the division.

 

A Possible Approach to Fraction Division Problems

 

The power of the multiplication/division relationship extends beyond elementary school. Students in grades 6 and up can use a multiplication equation with an unknown factor as a strategy for solving fraction division problems. Let’s consider this approach for two standard types of word problems and numerical division problems.

 

Let’s start with a word problem based on interpretation of division as finding unknown size of shares when the number of shares and the total are given.

 

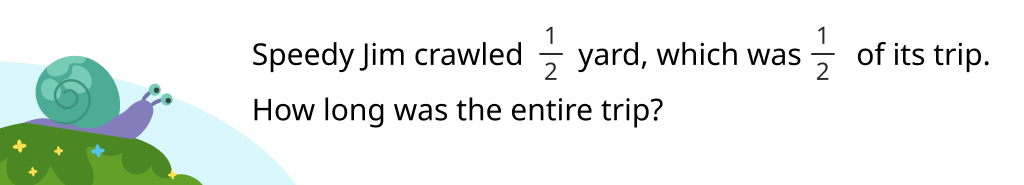
This is similar to a problem with given whole numbers. For example, “Jim crawled 6 yards, which was 3 of its regular daily trips. How long is the regular daily trip?” It’s interpreted as a problem with given total — 6, given number of shares — 3, and unknown size of the share. The original problem is often interpreted the same way, although the total is a fractional number (not really surprising), and there’s a fractional number of shares. Students have to get used to the latter, which is possible by considering examples of shares like a 2-gallon tank: 1 gallon is half of it, a quarter gallon is one eighth of it, etc.

The problem is solved by division 1⁄2 ÷ 3⁄4 = ▢, with the actual solution based on a model representing 1⁄2 as 2⁄4 and the division as 2⁄4 ÷ 3⁄4 = 2 ÷ 3 = 2⁄3. Simplifying the given fractions to a common denominator works for any fraction division problem. However, it is an extra step, which students can learn to eliminate later on when multiplying by the reciprocal fraction replaces direct division.

Let’s now take a look at an alternative strategy for solving the above problem.

The problem statement immediately translates into “Find the entire trip length ▢, given that 3⁄4 of it equals 1⁄2 yard.” Since 3⁄4 of ▢ is 3⁄4 × ▢, it’s an unknown factor problem

 

3⁄4 × ▢ = 1⁄2

 

related (equivalent) to the division problem 1⁄2 ÷ 3⁄4 = ▢.

To find the unknown factor, it is sufficient to single out the ▢ in the equation
3⁄4 × ▢ = 1⁄2. This is easily achieved by multiplying both sides of the equation by the reciprocal of a 3⁄4, that is by 4⁄3. (The reciprocal of any fraction is a fraction with numerator and denominator of the original fraction swapped. The reciprocal of a fraction times that fraction is always 1.) This multiplication results in

and the answer to the problem is:

▢ = 4⁄3 × 1⁄2 = 2⁄3

 

Consider now another type of a word problem.

 

No matter that the given total and size of the shares are fractions, this is a problem of finding an unknown number of shares: 11⁄2 ÷ 2⁄5= ▢. The original statement of the problem also translates into an unknown factor problem — the number of shares times size of the share equals the given total:

 

▢ × 2⁄5= 11⁄2

Alternatively, one arrives at the unknown factor problem starting with the division problem and using the relationship between multiplication and division. The unknown factor problem is solved as above by using the reciprocal fraction of 3⁄2.

 

As you can see, even fraction division problems can be understood and solved by relating them to multiplication.

 

***

Happy Numbers offers a curriculum in which students study mathematical procedures consistently. They increase and deepen knowledge using descriptive visual models, supplemented by manipulative mechanics and expressive animation. The immediate feedback integrated as hints allows students to improve their solving strategy in the moment, and thus learn from their own mistakes.

 

Happy Numbers can become a great digital assistant in your math lessons! Ready to join? Register as a teacher on the website to start a free trial period.