Building Conceptual Understanding through Multiple Representation, Modeling, and Manipulatives

Any student who can perform simple memorization can recall that 4 + 3 = 7. But what does it mean to truly understand the concept of addition? And how can teachers help students achieve this deep understanding?

In line with the latest research, we have found that the three pillars upon which conceptual understanding is built are multiple representation, modeling, and manipulatives. These interconnected approaches to teaching math help students understand the idea behind the answer, build math flexibility, and apply this understanding effectively.

 

Let’s look at an example using the commutative property of addition. This simply means that changing the order of addends doesn’t change the sum. It’s how we know that 4 plus 3 is equal 7 as well as 3 plus 4. This concept can be represented in word form, as above, written mathematically as formula a + b = b + a, or with the equation 3 + 4 = 4 + 3. These multiple representations are different ways of approaching the same mathematical understanding.

Add to this approach modeling, in which we expand the representation of this concept through visualization. Here, color-coding helps identify addends.

 

 

The powerful base-10 block model used here is presented as manipulatives so a student can move concrete blocks to interact with it in a personal way.

 

By integrating multiple representations, modeling, and manipulatives, we approach math concepts in a way that comprehensively shows the basis of mathematical thinking – a look under the hood, if you will. According to Adding It Up, published by National Research Council, “students with conceptual understanding know more than isolated facts and methods. They understand why a mathematical idea is important and the kinds of contexts in which is it useful.” Through conceptual understanding, mathematics becomes a well-organized cumulative knowledge that a person can apply to various concrete situations. With conceptual understanding, students fully grasp the connections between math facts, rules, and principles and can create specific solutions without losing their actual meaning. It’s a powerful web of math ideas forming an organic whole that’s strongly connected with student math experience. Through practice, the web becomes stronger, and a student achieves fluency operating with it.

 

Here’s a sneak peek at how Happy Numbers incorporates the three pillars of multiple representation, modeling, and manipulatives.

 

 
… is used to show the same math concept in different ways. For example, we can record the equation 3 × 4 = 12 using numbers and symbols. Or it can be written in word form: “three times four equals twelve.” Here’s an example of how the Happy Numbers Grade 3 curriculum uses both of these representations, along with a picture and repeated addition:

 

 

Multiple representations are widely used to build meaning behind math and develop a deeper understanding of properties or ideas connected to the same fact or operation. Representations include words, symbols, graphs, diagrams, tables, formulas, physical and virtual manipulatives, etc. They can be applied to math tools like the number line, a hundred chart, or a place value table. These representations help students consider features from different perspectives and extend their math experience.

 

 

It’s not always obvious, but math is all around us. Each time you’re cooking, you measure the quantity of ingredients and watch the time. To determine when to set your alarm clock, you’ll calculate hours of sleep. For elementary school math lessons, it’s very helpful to model tasks with concrete scenarios. Look how 5th graders help Dino develop his cooking talents:

 

 

According to CCSS, “Mathematically proficient students can apply the mathematics they know to solve problems arising in everyday life.” So it’s not only an important skill but the standard which students need to grasp and apply in practical situations.

 

 

By the 19th century, scientists, methodologists, and teachers identified the effectiveness of learning through tangible experience. They developed and proved the positive impact of manipulatives — a palpable way to model multiple representations of math concepts. Among researchers and practitioners, you’ll find names such as Maria Montessori, Jean Piaget, and contemporary psychologist Jerome Bruner. Manipulatives provide students with engaging physical experience without losing attention to education. They can be represented as real objects, like toys in a classroom, as well as more abstract digital visualizations, like Place Value Disks.

 

 

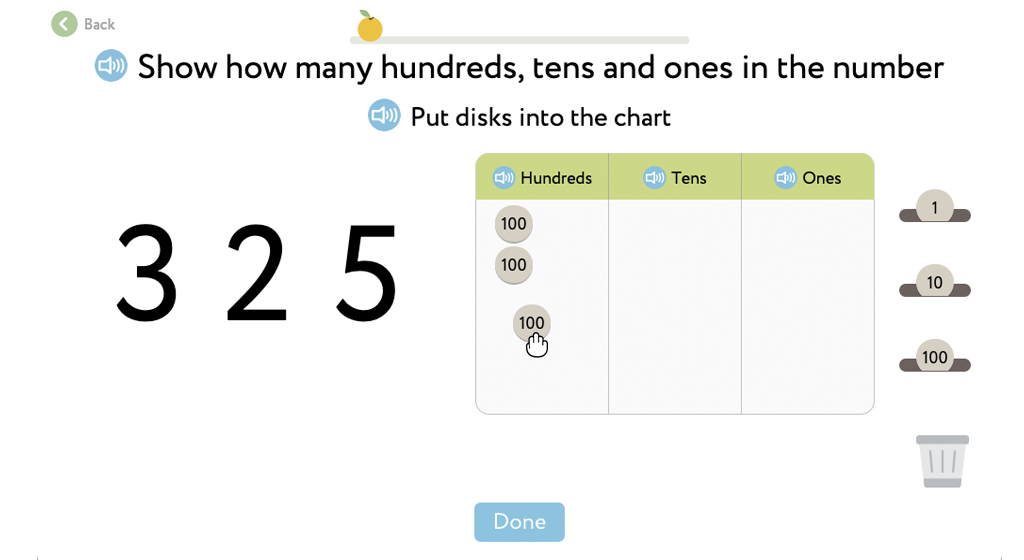
Multiple representations, modeling, and manipulatives provide students a full immersion into math. Instead of learning intangible facts, they get a comprehensive conceptual view that cultivates math mindset. This enables math flexibility, effective problem-solving, and a logical approach to everyday situations.