Comparison of Whole Numbers within 1000

In Pre-K and Kindergarten, students learn a lot about numbers: their names, notation, sequencing, and counting. With a foundation of different visual representations, they grasp that each number can answer the question, “How many objects are in a group?” This logically brings students to a new mathematical skill, comparison.

There are two widely-known pedagogical approaches to make comparison intuitive and easy to master, and between them, Happy Numbers chooses both. Each approach allows students to look at comparison from a different angle, so together they complete the picture and effectively develop the skill.

The first approach is built on modeling numbers with sets of objects and comparing those sets. For example, students establish one-to-one correspondence of one of the sets with a part or the whole of the other:

To see the full exercise, follow this link.

 

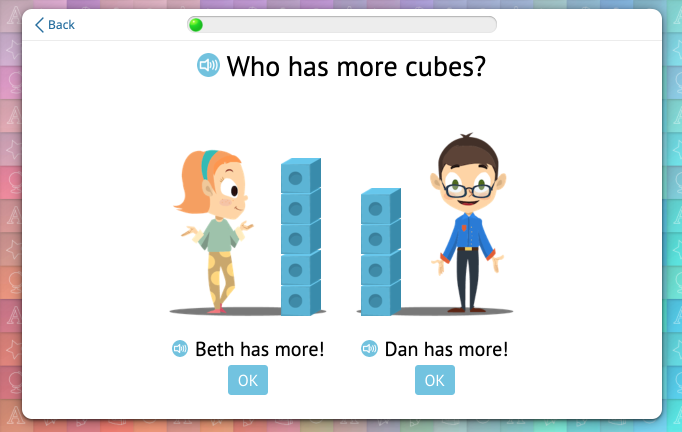
This approach is the most effective for the initial introduction of the concept. Learn about it in detail in this article on the Happy Numbers blog. Moreover, comparison of object sets remains useful as long as modeling with objects is visually simple. Happy Numbers even uses it in comparing pairs of two- and three-digit numbers later in the curriculum.

The second approach connects the greater than – less than concept with the counting sequence, using the Number Line as a visual representation. At the initial stage of math education, this approach is beneficial for comparison of two-digit numbers. Students grasp Number Line modeling as a form of comparison, which prepares them to use it for more complicated tasks in the future.

Students start with comparison of two-digit numbers supported by a model of Base-10 Blocks:

 

 

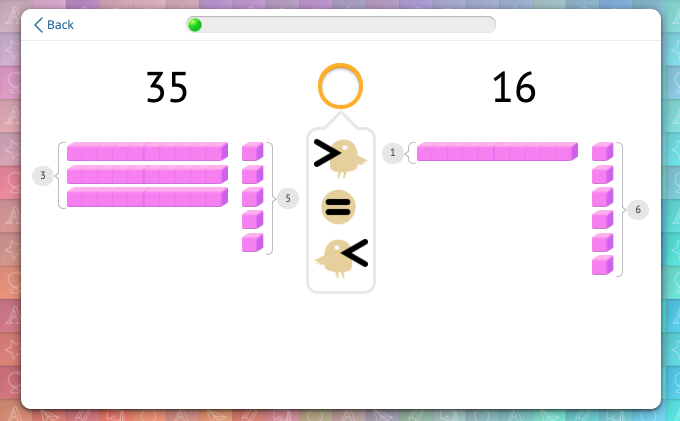
The solving strategy here is based on the meaning of the tens and ones digits, which Happy Numbers supports by including a Base-10 Block model in the problem statement. Students encounter several tasks with two kinds of given numbers: those with an equal number of tens and those without.

 

When students successfully complete this highly-supported exercise, Happy Numbers reduces the scaffolding. Now, visual models are removed from the problem statement, and the task looks like this:

 

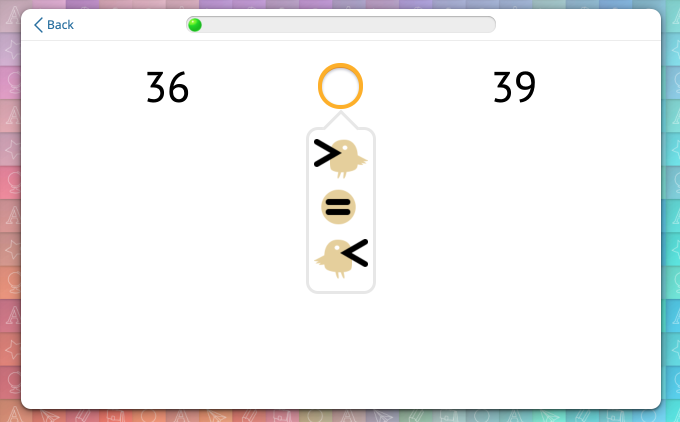
If the submitted answer is not correct, students receive full support: Base-10 Block models for the numbers are provided.

To see the full exercise, follow this link.

 

Support is only provided to those who need it. When students master the skill, they get the green light for the next topic.  

 

 

Now let’s take a look at the comparison strategy for two-digit numbers based on the greater than –  less than concept and the Number Line visual model.  

 

According to the Happy Numbers curriculum, students encounter this type of comparison in Grade 1. By this time, they are typically well-versed in counting to 100. Since the first hundred is conquered, they are ready to:

– Easily understand that a number appearing later in the counting sequence is greater than a number that appears earlier.

– Apply their proficiency in counting to identify which of two given numbers is greater.

 

Happy Numbers represents the counting sequence with the Number Line, and students get used to the visual model by working on exercises like these:

 

 They start to compare numbers by marking them on the Number Line:

 

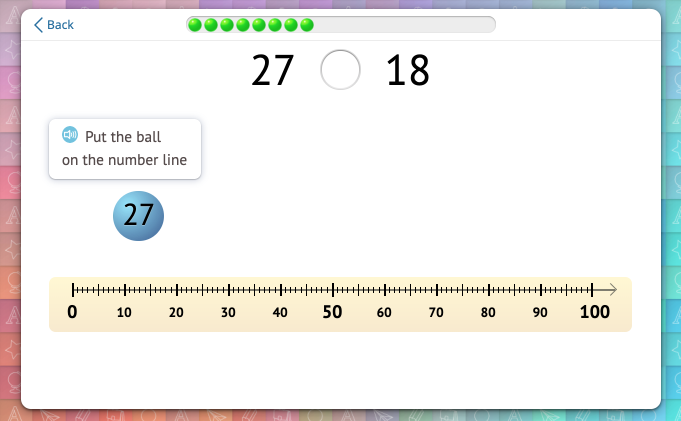
 Looking at the numbers placed on the Number Line, students choose the sign:

 

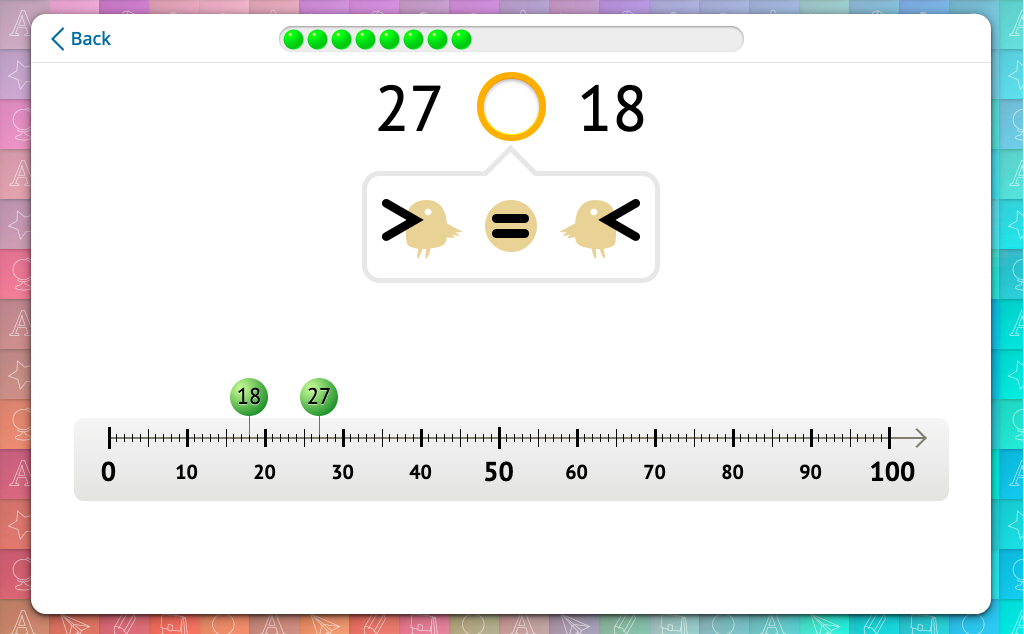
If students answer incorrectly, the sign flashes red. The student has to choose again.

To see the full exercise, follow this link.

 

As with all Happy Numbers exercises, students must solve several similar tasks in order to show mastery. “Similar tasks” means that the math problems differ only in the numbers given. Each task is considered solved if students give the correct answer on the first attempt. The entire exercise is considered successfully completed if, for example, a student solves 3 tasks in a row or 4 of 5 consecutive tasks. When students successfully complete the exercise, Happy Numbers gradually removes the scaffolding from future exercises.

 

On the next level of difficulty, Happy Numbers still keeps the Number Line on the screen as a hint, but this time the task doesn’t require marking the numbers on it:

 

After the successful completion of this exercise, students move forward. They are now required to give the answer without a visual hint:

 

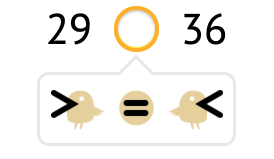
In case of an incorrect answer, students receive visual support: the Number Line with both numbers placed on it.

To see the full exercise, follow this link.

The strategy introduced here is based on counting skills that are already well-developed, which boosts fluency in comparing two-digit numbers.

 

In addition to that, the association that greater than means farther to the right on the Number Line makes comparison more intuitive. For example, it helps students grasp that any three-digit number (even 100!) is greater than any two-digit number.

 

 

Even if the difference between two- and three-digit numbers may seem obvious, it’s still important to break it down in detail for students. Happy Numbers starts by focusing them on two-digit numbers and three-digit numbers as distinct types:

 

To see the full exercise, follow this link.

 

Some students are experienced with the Number Line and know that whole numbers farther to the right are greater than those closer to 0. These students will easily see that any two-digit number is less than any three-digit number. Here, all students will discover this fact by modeling the numbers. Watch the video to see how Happy Numbers leads students to this conclusion.

 

In brief, they enter any pair of two- and three-digit numbers that comes to mind and answer simple questions, which keeps them involved.

Students then complete an exercise solidifying the skill of comparing two- and three-digit numbers:

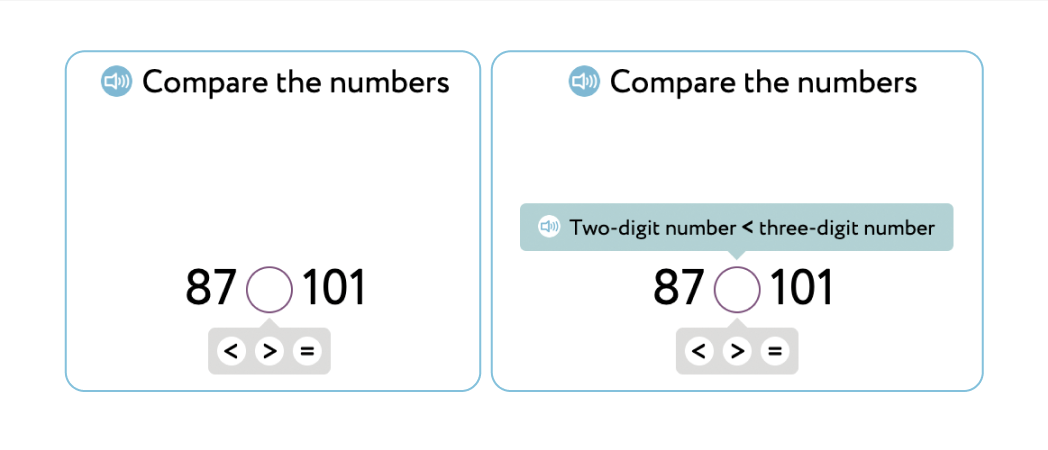
Students choose the sign and receive support in case of an incorrect answer.

 

We present each type of comparison, as shown by this task with the three-digit number on the left:

To see the full exercise, follow this link.

 

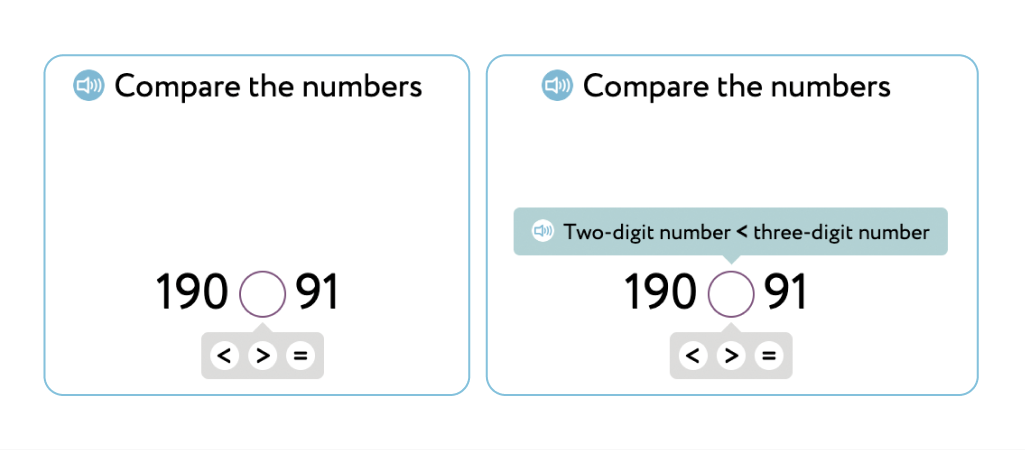
Students encounter the three types of comparisons in quasi-random order, so that the sequence of answers >, <, and = doesn’t follow any obvious pattern.

These types of tasks promote recognition that for any numbers a and b:
a being less than b is equivalent to b being greater than a.

 

 

Comparison of multi-digit numbers can be performed as a place-by-place procedure (similar to addition), comparing digits one place at a time. So, the focus of mastering the comparison is on:
– Knowing where to start.
– Standard procedure at each place.
– Deciding where to stop.

 

The last of these is important for comparison, which is different from addition where moving to the next place continues until all places are worked on. It’s also worth mentioning the contrast to addition (at least to the standard algorithm) by working from left to right when comparing.

 

The Happy Numbers Grade 2 curriculum includes comparison of two three-digit numbers, providing an assortment of exercises rich enough to develop conceptual understanding and prepare students to compare multi-digit numbers.

 

 

This introductory task is the simplest type of comparison of three-digit numbers. To make it easy to grasp, Happy Numbers models the numbers with the visual support of Base-10 Blocks in the problem statement:

 

 

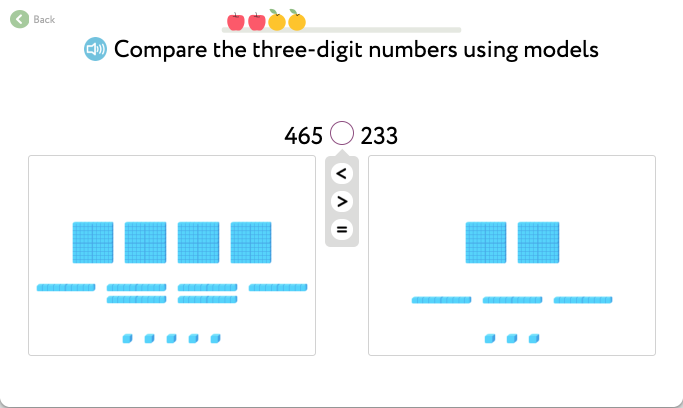
When students answer correctly, they receive a statement that emphasizes the pattern behind the result:

 

To see the full exercise, follow this link.

 

In case of an incorrect answer, students receive the same statement as a hint.

After this exercise, Happy Numbers introduces new scaffolding — the next step from manipulatives to mastery. Watch how the animation transforms the given problem:

 

Happy Numbers provides another representation of given numbers in the form of Place Value Cards. Once again, our software brings this representation to life as animation draws out the value of each digit.

 

 

… and then adds a hint:

 

 

If students compare hundreds correctly, they will be asked to give an answer to the original problem:

 

To see the full exercise, follow this link.

 

Moving from comparison of hundreds to the original problem is an implicit hint: when a pair of three-digit numbers has different hundreds, their comparison stops. The greater number is recognized as the one with more hundreds.

The next exercise requires students to give the answer without any hints:

To see the full exercise, follow this link.

 

Happy Numbers will only provide a hint in case of an incorrect answer. The hint here shows both numbers represented by Place Value Cards, just like before, so the student continues working with the scaffolding to master the skill. At the same time, to successfully complete the exercise, students have to meet a certain threshold of solving tasks without hints.

 

Comparing a pair of three-digit numbers with equal hundreds

 

Happy Numbers introduces this topic with a series of three exercises. In the first one, the scaffolding uses Base-10 Blocks to represent the problem statement and provides a hint if a student submits an incorrect answer:

To see the full exercise, follow this link.

In the second exercise, the visual model of Base-10 Blocks is replaced by Place Value Cards:

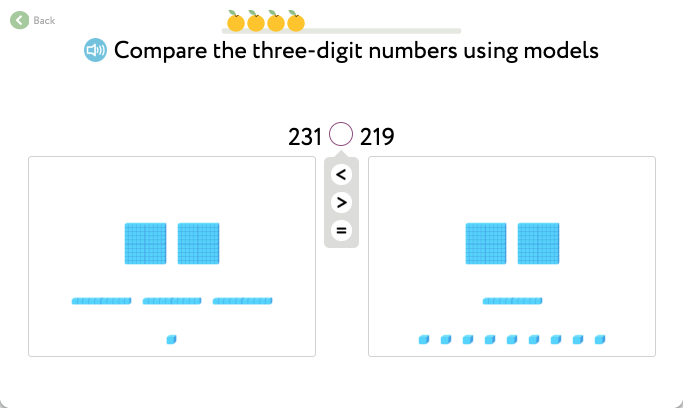
Since in this case the number of hundreds is the same, the comparison goes on to tens:

When the tens are different, students have everything they need to compare the numbers given:

When the tens are the same, the next step is comparison of ones:

To see the full exercise, follow this link.

 

To solidify the skill, Happy Numbers reduces the scaffolding incorporated in the problem statement. First, the hints are removed, and then the Place Value Cards are removed too. Finally, in the last exercise, the tasks look like this:

 

To see the full exercise, follow this link.

 

In Grades 1 and 2, Happy Numbers provides highly interactive content that helps students:
– Gain the conceptual understanding of comparison of whole numbers based on place value and the Number Line representation.
– Grasp efficient skills to compare numbers within 1,000.

 

Students are prepared to learn more advanced skills and solve more complicated tasks comparing multi-digit numbers.

 

 

Understanding of comparison is a lot deeper than it appears at the surface. By comparing shapes, attributes, quantities, measurements, and numbers, students develop abstract thinking skills, which also influences their creative mindset. Surprisingly, this is how language gets all its poetic similes, like “as clear as crystal” or “as graceful as a swan.” Aren’t these also comparisons? Yes, they are! Mathematicians need to be very accurate in building research, theories, and proofs, but math simultaneously contributes to understanding of intangible abstract relationships in the world around us.

 

Happy Numbers develops curriculum that provides teachers with comprehensive assistance to build meaning behind math for their students. Join for free and see firsthand how your students improve their understanding of comparing numbers.